Hans Lauwerier - Symmetrie, kunst en computers

Aramith - Haarlem

Hans Lauwerier is emeritus hoogleraar in de toegepaste en zuivere wiskunde, en auteur van boeken als Fractals, Symmetrie, Een wereld van fractals, Oneindigheid en Computersimulaties.

Inhoud

Voorwoord 7
1. Inleiding 11
2. Groepen 24
3. Decoraties in het platte vlak 37
4. Tegelpatronen 49
5. De tegels van Penrose (De gulden snede) 63
6. De platonische lichamen 72

7. Halfregelmatige lichamen 83
8. Sterren 98
9. Computerkunst 104
Bibliograﬁe 115
Register 117
Over de diskette 119
Illustratieverantwoording 120

Voorwoord
Het boek dat u nu in handen heeft, is te beschouwen als vervanger en opvolger van de in 1988 verschenen uitgave over symmetrie van dezelfde auteur. Maar het is veel meer dan een herziene en bijgewerkte versie van dat inmiddels uitverkochte boek. In de eerste plaats is er op het gebied van symmetrie het een en ander gebeurd.
De door de Engelse wiskundige Penrose ontworpen tegels, berustend op de symmetrie van de regelmatige vijfhoek - ooit begonnen als spelletje - bleken fundamenteel nieuw inzicht te geven in de structuur van materie. Chemici ontdekten nieuwe bouwstenen in de koolstofchemie, zogenaamde fullerenen of voetbalmoleculen. In de stereometrie waren zulke halfregelmatige ruimtelijke vormen reeds bekend als archimedische lichamen. Redenen genoeg om er in dit nieuwe hoek ruim aandacht aan te besteden.
Het belang van symmetrie in de beeldende en de decoratieve kunst moge bekend zijn. Veel technisch werk van de kunstenaar kan tegenwoordig door de computer worden overgenomen. De technische mogelijkheden van de computer zijn dermate verbeterd, dat het niet moeilijk meer is binnen luttele minuten de meest prachtige symmetrische vormen op het beeldscherm te krijgen. Dat geldt in het bijzonder voor de huiscomputer waarbij men de beschikking heeft over een oplossend vermogen en een snelheid die vroeger alleen voorbehouden waren aan de kostbare computers die in de wetenschap en de industrie worden gebruikt. De kleurenillustraties in dit boek geven daarvan de neerslag. U zou ze kunnen zien als voorbeelden van computerkunst, maar dan dient u wel te bedenken dat de eigenlijke kunstenaar de wiskunde zelf is.
In feite is er niets anders gedaan dan te trachten de eenvoudige structuren die in de wiskunde voorhanden zijn, voor het mensenoog zichtbaar te maken. Wie enigszins bekend is met de Mandelbrotﬁguur, weet dat de prachtige beelden die daarin verscholen liggen uiteindelijk door een heel eenvoudig wiskundig recept bepaald zijn. Datzelfde geldt voor de veelsoortige fractals die de naam van de Franse wiskundige Julia dragen. Om ruimte te bieden aan de nieuwe onderwerpen zijn van het oude boek onder andere een aantal al te technische passages weggelaten. Computerprogramma's, vroeger in het boek opgenomen, zijn nu verzameld op een diskette, die bij dit boek is ingesloten. Van sommige programma's is op de diskette ook een wiskundige beschrijving gegeven. Wij hopen dat hiermee de leesbaarheid is toegenomen.
Het eerste hoofdstuk is een kennismaking met het begrip symmetrie aan de hand van voorbeelden uit de ons omringende wereld: wat in vervlogen eeuwen door mensenhand geschapen is, zoals decoraties op eeuwenoud aardewerk en objecten van de levende en levenloze natuur, bijvoorbeeld een bloem, een kristal.
In dit boek ligt het accent enigszins op het wiskundige begrip van de 'groep', dat wiskundige abstractie van symmetrie. Een groep is een eenvoudige, maar toch rijke wiskundige structuur, die het mogelijk maakt de vele vormen van symmetrie te analyseren en te classiﬁceren. In het tweede hoofdstuk wordt hier de nodige aandacht aan besteed. De behandeling van dit uiterst belangrijke begrip is enigermate gepopulariseerd, zodat het ook voor de niet-mathematisch geschoolde lezer toegankelijk is. Het kan zijn dat sommige passages bij eerste lezing een beetje droog en technisch lijken, maar laat u zich daardoor niet weerhouden verder te lezen. Voor een deel is het niets anders dan wennen aan een bepaalde, nauwkeurige terminologie die in de natuurwetenschappen alom gehanteerd wordt. Let vooral op de rotatiegroep en de diëdergroep, waarbij we de symmetrie van bijvoorbeeld de swastika of het zonnerad en de hoofdletter X of het plusteken kunnen aangeven met de notaties C4 en D4.
De echt interessante zaken nemen een aanvang in hoofdstuk 3, waar de symmetrie van een regelmatig vlak patroon wordt onderzocht. De Egyptische grafschilderingen uit hoofdstuk 1 keren hier in abstracte vorm terug, evenals de meanderrand. Ook vindt u er de theoretische achtergrond van menige Escherprent.
Tegels laten een speciale vorm van een regelmarig patroon zien. Omdat er zoveel over te verrellen is, hebben we er twee hoofdstukken aan gewijd. In het vierde hoofdstuk betreft het de klassieke patronen die teruggaan op Archimedes en die onder andere door Johannes Kepler uitvoerig zijn beschreven.
In het vijfde hoofdstuk gaat het vooral om de quasiperiodieke vijftallige tegelpatronen van Penrose. Ze zijn gekarakteriseerd door het guldensnedegetal en nauw verbonden met het pentagram. Overigens was het pentagram, ooit beladen met mystiek, een der favoriete ﬁguren van Kepler.
In dit boek is ook meer aandacht besteed aan ruimtelijke symmetrieën, aan de veelvlakkige vormen waaraan de namen van Plato en Archimedes zijn verbonden. De vijf regelmatige veelvlakken, de zogenaamde platonische liehamen, worden beschreven in hoofdstuk 6. Eens werden zij beschouwd als de bouwstenen van het heelal, en werden hun afmetingen door Kepler in verband gebracht met de planeten van ons zonnestelsel. Nu, aan het einde van de twintigste eeuw, weten we dat sommige virussen, partikeltjes op de grens van de levende en de levenloze natuur, precies volgens een dergelijk meetkundig veelvlak gevormd zijn.
De beschouwingen worden voorrgezet in het zevende hoofdstuk, waarin de halfregelmatige lichamen de revue passeren. Ook hier zijn Archimedes en Kepler goede gidsen. Enkele van die lichamen zijn recentelijk populair geworden - in de sport als voetbal en in de koolstofchemie als een nieuw molecuultype, een zogenaamd fullereen.
Inzicht in ruimtelijke symmetrische ﬁguren steunt voor een belangrijk deel op goede illustraties, op het maken van een projectie van een ruimtelijke structuur op een plat vlak. Nu de computer zoveel mogelijkheden biedt en we de beschikking hebben over goede software, is dat niet moeilijk meer. De afbeeldingen die in ruime mate de tekst begeleiden, zijn alle met de huiscomputer gemaakt. Met de programma's op de diskette kunt u ze thuis namaken. De beste manier om een ruimtelijk object te zien, is om er als het ware omheen te lopen, het van verschillende zijden te beschouwen. Voor het beeldscherm van een computer zittend kunt u dat imiteren door in hetzelfde programma telkens een andere kijkrichting te nemen, een verandering van slechts twee getallen.
Dankzij de computer is het ook veel gemakkelijker geworden om inzicht te verwerven in de zogenaamde sterveelvlakken. Kepler merkte al op dat de vijf platonische liehamen niet compleet waren wanneer men de eis van convexiteit liet vallen. Hij ontdekte het bestaan van twee sterachtige lichamen die konden worden opgebouwd uit elkaar doordringende pentagrammen. Veel later, in de negentiende eeuw, werden door Poinsot nog twee van die sterren ontdekt, waarmee de serie compleet was. In dit boek zijn die vier sterren afgebeeld in grijstinten, waarbij de kleurgradatie gekoppeld is aan de richting van de lichtbron. Tevens bespreken we in dit achtste hoofdstuk een paar zogenaamde compounds, waarbij een aantal regelmatige lichamen of vlakdelen elkaar op regelmatige wijze doordringen.
Het negende en laatste hoofdstuk heeft betrekking op computerkunst. Ook los van de wiskundige of technische interpretatie van een symmetrisch plaatje kan een symmetrische ﬁguur gewoon mooi zijn. Of we een dergelijk plaatje als kunst mogen beschouwen, laten we in het midden. Omdat we in dit boek in de regel uitgaan van eenvoudige wiskundige begrippen, is de wiskunde de enige kunstenaar. Het doet denken aan het bekende verhaal van Newton, die zijn ontdekkingen beschreef als het oprapen van mooie schelpen op een exotisch strand. Ook hier hebben we in de rijke wiskundetuin slechts enkele bloemen geplukt en ze in de vorm van kleurenillustraties in dit boek opgenomen. In dit laatste hoofdstuk gaan we ook kort in op de technische achtergrond van deze afbeeldingen. Met de programma's op de diskette is het mogelijk menige symmetrische voorstelling te creëren. Wie de structuur van de programma's enigszins doorziet, kan met een andere keuze van parameterwaarden soortgelijke en soms heel andere plaatjes maken.
terug naar de Inhoud

1. Inleiding

1.1 Griekse schaal met meanderrand

Symmetrie, het woord zegt het al. Op klassiek Griekse wijze samengesteld uit een voorvoegsel dat de betekenis van 'samen' heeft en het begrip 'meten', duidt het op: een 'samengaan van maten'. Dat kan in zijn eenvoudigste vorm betrekking hebben op de spiegelsymmetrie waarin de natuur de hogere vormen van leven heeft gevormd, maar het kan ook een zich herhalende versiering van antiek vaatwerk of de decoratie van een Egyptisch grafgewelf zijn. In ﬁguur 1.1 zien we bijvoorbeeld een vroegGriekse schaal met de bekende meanderrand. We zien ook dat de kunstenaar een beetje moest smokkelen om de randversiering na een rondgang tot sluiting te brengen.
Van de vroege Egyptische beschaving zijn we vrij goed op de hoogte. De Egyptenaren plachten veel met onvergankelijk materiaal te werken en zagen er niet tegenop in hun stenen monumenten uitvoerige teksten te beitelen in het door hen uitgedachte hiërogliefenschrift. En wanneer zij op meer vergankelijk materiaal zoals papyrus schreven, zorgde het kurkdroge woestijnzand voor een langdurige conservering.
De Egyptische kunstenaars waren zeer bedreven in de beeldende kunst en zowel in hun bouwwerken als in hijvoorbeeld hun grafdecoraties lieten zij zich leiden door meetkundige principes van herhaling en symmetrie. In ﬁguur 1.2 laten we een tweetal fragmenten zien van de versiering van een Thebaans grafgewelf. Het is stellig een intellectuele uitdaging dergelijke meetkundige patronen te analyseren en te rubriceren. Het doet denken aan het beschrijven van kristallen, regelmatige ruimtelijke patronen, maar nu gaat het om wat we tweedimensionale kristallen zouden kunnen noemen. Met de methoden van de kristallograﬁe, in het bijzonder de groepentheorie, zijn we in staat tot een goede classiﬁcatie, waarop we later uitvoeriger terugkomen.

1.2 Symmetrische versieringen in een Egyptisch graf

De eenvoudigste manier om vlakversieringen als deze te analyseren, is om te letten op de herhalende elementen, op het kleinste fragment dat door verschuiving kan worden herhaald. Bij het linkerpatroon kunnen we de ﬁguur opdelen in vierkanten met horizontale en verticale zijden, waarbij hoekpunten de centra van de dubbelspiralen zijn. Twee naburige vierkanten zijn in wezen identiek, maar verschillen in een kwartdraai. Tezamen kunnen ze een herhalend element zijn. Maar ook kan men een herhalend element samenstellen als een schuin vierkant met vijf spiraalcentra, geplaatst volgens de vijf van een dobbelsteen.
Om een eventuele spiegelsymmetrie te detecteren is het vaak handig om te letten op de draaizin van de in het patroon aanwezige spiralen. In beide ﬁguren treffen we zowel naar links als naar rechts draaiende spiralen aan. De symmetrie omvat daarmee dus in elk geval een spiegeling.
Zonder hulp van een beetje wiskunde is het lastig tot een juiste classiﬁcatie te komen, maar met het materiaal van de volgende twee hoofdstukken is dat niet meer moeilijk. Het belangrijkste resultaat van het moderne theoretische onderzoek is, dat er precies zeventien manieren zijn om een vlak op symmetrische wijze met repeterende motieven te vullen. Het is een klein wonder dat de meeste daarvan reeds in de Egyptische decoratieve kunst zijn terug te vinden.

Antiek aardewerk
Nog vroeger in de kunstgeschiedenis kan men objecten aantreffen waarbij nijvere ambachtslieden als pottenbakkers hun produkten verfraaiden met symmetrische voorstellingen. Van de bewoners van Tweestromenland in de vijfde eeuw v.Chr. weten we maar weinig af. Schriftelijke getuigen zijn er nog niet, maar scherven des te meer. In ﬁguur 1.3 beelden we een schotel af opgegraven in de omgeving van Samarra, een klein dorpje ten noorden van Bagdad.
De decoratie doet ons denken aan molenwieken, een symmetrievorm die technisch beschreven kan worden als een viertallige rotatiesymmetrie. Het middelpunt van de schotel kunnen we opvatten als een centrum waaromheen de schaal in gedachten gedraaid kan worden. Telkens na een kwartdraai is de decoratie globaal hetzelfde gebleven, de motieven herhalen zich bij elke kwartdraai. Ook zien we weer de meanderrand, symbolische rimpelingen van een wateroppervlak misschien. In elk geval zien we vissen zwemmen en vogels die de vissen vangen. Een wel zeer vroege voorloper van de vis-en-vogelprenten van Escher. Bij andere schalen zien we soortgelijke motieven en zijn er overeenkomstige draaiingssymmetrieën. Soms zijn de motieven ook spiegelsymmetrisch. Kortom, aan oud aardewerk is heel wat te beleven.
Symmetrie is een belangrijk element in de decoratieve kunst, getuige de ontelbare objecten die de mens in zijn bestaan op kunstzinnige wijze heeft versierd. Blijkbaar wordt onze geest aangenaam getroﬂen door het element van herhaling, wanneer wij een symmetrische vorm beschouwen. Het is een soort herkenning, alsof we een vertrouwd persoon begroeten die we reeds eerder hebben leren kennen. Datzelfde gevoel hebben we bij het beluisteren van muziek, een volkslied met refreinzang of de kunstige variaties op een thema van Bach.
Symmetrie in de vorm van een zich steeds herhalende structuur treffen we ook aan in dat dichtkunst, in de grote epen van de klassieke oudheid en in religieuze gezangen. Eens luisterde een grote schaar van mensen naar de vertelkunst van de Kelten. Helaas is daarvan nauwelijks iets op schrift overgeleverd. We kunnen vermoeden dat de barden zonder technische hulpmiddelen, slechts beschikkend over een in onze ogen onbegrensd geheugen, hun verhalen konden vertellen. Uiteraard maakten ze gebruik van vaste patronen en structuren, rijm en metrum als zich herhalende elementen. Die symmetrie in ruimere zin ondersteunde hun mentale vermogens en was ook belangrijk voor de toehoorder, die er zijn verwachtingspatroon op baseerde. In onze tijd zijn er nog steeds geheugenkunstenaars, die urenlang de verzen van de klassieke Hindoeliteratuur, Mahabharata en Ramayana, weten te reciteren.
In dit boek houden we ons vooral bezig met de visuele aspecten van symmetrie, met wat natuur en kunst ons bieden. Kunst is een moeilijk te deﬁniëren begrip. Een objectieve definitie bestaat niet en kan ook niet worden gegeven. Elke interpretatie van kunst is gebonden aan tijd en cultuur.
Wellicht kan men op een meer zinnige wijze spreken van bepaalde vormen van (toegepaste) kunst. Zo kan men al varend ﬁlosoferen over een rij golfjes en zal men later zijn vaatwerk op decoratieve wijze voorzien van een meanderrand, een abstracte versie van het golvende water dat men zo vaak heeft gezien. In ﬁguur 1.4 tonen we een meanderrand zoals de Romeinen die hebben toegepast in hun mozaïeken (ca. 220 n.Chr.). Misschien dachten de Romeinen, ver van huis, in Keulen bijvoorbeeld, daarbij onbewust aan de golfjes van de Middellandse Zee.

De Arabische wereld
Het blijft nog steeds een wonderlijke zaak dat het culturele erfgoed van de Grieken en de Romeinen pas met een vertraging van vele eeuwen in de westerse wereld nieuwe impulsen kreeg. Voordat bij ons, en met name in Italië, de renaissance een aanvang nam, was er een nieuwe Arabische cultuur opgebloeid waarin kunst en wetenschap de volle aandacht kregen. Arabische geleerden vertaalden de geschriften van de Grieken, zetten het werk van Aristoteles voort en leverden bijdragen aan wiskunde en sterrenkunde. In hun godsdienst was geen plaats voor de afbeelding van godheden en schutspatronen, maar als een soort compensatie ontwikkelden de Arabieren een op meetkundige principes gebaseerde decoratieve kunst.
In ﬁguur 1.5 zien we een voorbeeld van Arabische decoratieve kunst, een raam van een moskee te Mazar met ster- en bloemvormige motieven.
In het derde hoofdstuk, ﬁguur 3.12, zie we een fraai detail van een raamversiering van een moskee in Kaïro uit de veertiende eeuw. Het is een ingewikkeld symmetrisch patroon waarin van alles te ontdekken is. Op het eerste gezicht zien we rechthoeken die op een vreemde manier in elkaar grijpen. Beter kijkend zien we driebladige motieven, trifolia, die aan elkaar zijn geschakeld. Het beschrijven van een dergelijke gecomplieeerde symmetrievorm is zonder wiskunde, zonder gebruik te maken van het wiskundige begrip 'groep', niet goed mogelijk. In hoofdstuk 3 zullen we zien hoe we dergelijke symmetrische patronen kunnen analyseren en classiﬁceren. Vooruitlopend op de behandeling van vlakke symmetrievormen kunnen we constateren dat het moskeeraam tot het type p6, uit de bijenraatfamilie, behoort. Wie nu al wil experimenteren moet de afbeelding eens over een hoek van zestig of 120 graden draaien en kijken of dat verschil uitmaakt. Ook kan men de ﬁguur spiegelen, door hem met een zakspiegeltje te bekijken. Blijkbaar heeft ook dat geen invloed, de ﬁguur (in gedachten naar alle kanten voortgezet) blijft hetzelfde.
Moderne kunstenaars als M. C. Escher en H. Hinterreiter maakten reeds in hun jonge jaren een soort pelgrimstocht naar het Alhambra, het rode fort van de Moren. Als menige andere bezoeker waren zij diep onder de indruk van de fraaie symmetrische patronen waarmee de Moorse heersers van Spanje hun paleizen plachten te versieren. In ﬁguur 1.6 nemen we een kijkje in het Alhambra. De voorstelling is zelf al symmetrisch, maar wanneer we voor de vele met tegels bedekte wanden staan, ontdekken we veel meer symmetrieën.

Tegels
De tegelpatronen van de Arabieren dienden als voorbeeld voor pottenbakkers in Spanje en Italië, en later in de Nederlandse gewesten. Aanvankelijk waren de decoraties nog zuiver geometrisch van aard, maar de Hollandse tegelbakkers in de zestiende en zeventiende eeuw zouden ze voorzien van ﬁguratieve voorstellingen - vogels, vissen, mensen en bloemen, om maar iets te noemen. De tegels dienden vooral ter verfraaiing van dat stookplaats, de keuken, trap en gangen.
In zeker opzicht kan de structuur van de in het patroon aanwezige symmetrie dienen als indicatie van tijd. Hoe ouder de tegel, des te rijker de symmetrie. Een enkele tegel is al mooi om te zien, maar wanneer de tegels in blokken van vier, zestien of meer worden verenigd, zien we pas de rijkere structuur die ontstaat wanneer de herhaling mede een rol gaat spelen. We zien dan ook dat de hoekelementen van de tegels een patroon gaan vormen dat bij een enkel exemplaar nog niet opviel. Tegelverzamelaars streven er dan ook naar om van een enkel tegeltype zoveel exemplaren te bemachtigen, dat ze er blokken van kunnen vormen. In bijvoorbeeld het museum Het Princessehof te Leeuwarden kan men indrukwekkende tegeltableaus zien, ooit door notaris Nanne Ottema uit talloze nalatenschappen bijeengebracht. In ﬁguur 1.7 tonen we een blokje van vier vroegSpaanse tegels met de typische Arabische ornamentiek.
Een late tegenhanger is bij ons de zogenaamde Haarlemmer tegel, zoals getoond in ﬁguur 1.8. Een enkele tegel heeft het symmetrietype van een vierkant, een vorm die we later als D4 zullen beschrijven. Men kan zich voorstellen welke werking er uitgaat van het samenspel van hoeken en randen wanneer meer tegels naast elkaar zijn geplaatst.
Bij latere tegels is de geometrische symmetrie nagenoeg afwezig, gebleven is slechts de herhaling van een zelfde voorstelling, een landschap bijvoorbeeld, of een bijbelse voorstelling.

Architectuur
Er zou een heel boek kunnen worden geschreven over de symmetrieën die we bij bouwwerken aantreffen. We zouden kunnen beginnen met de Egyptische piramiden en vervolgen met de Griekse tempels, waarin ook het element van herhaling aanwezig is. Een hoogtepunt zou misschien het Pantheon te Rome zijn. Eenvoudiger symmetrieën treffen we aan bij de vele kerken en kathedralen die een kruisvorm bezitten.
Heel opvallende symmetrieën kunnen we zien in de roosvensters van de talloze kathedralen van
de late middeleeuwen. Hier beperken we ons tot een enkel voorbeeld en we laten het aan de reiziger over meer van dergelijke objecten zelf te ontdekken. In ﬁguur 1.9 tonen we als een enkel voorbeeld een roosvenster van de kathedraal van Orvieto. Van binnen uit gezien vertonen kerkramen vaak een bonte kleurenpracht waarin religieuze en profane elementen onze aandacht trekken. Met de programma's van de begeleidende diskette zijn we in staat zo'n roosvenster als een abstract symmetrisch patroon, een fractal, op kleurrijke wijze te simuleren. In ﬁguur 1.10 in het kleurkatern is daarvan een voorbeeld gegeven.

Kristallen
De natuur voorziet ons van een groot aantal symmetrische structuren. De stoffelijke wereld is opgebouwd uit moleculen die intern al een bepaalde symmetrische structuur bezitten. Elementaire krachten rijgen de afzonderlijke moleculen aaneen tot bouwwerken die we kristallen noemen. Een enkel kristal heeft de vorm van een meetkundig veelvlak, waarin de symmetrieën van de samenstellende moleculen terug te vinden zijn. We kennen allemaal de elementaire vormen van het regelmatige viervlak (tetraëder), kubus en regelmatige achtvlak (oktaëder).
Een methaanmolecuul is gevormd als een koolstofatoom omringd door vier waterstofatomen op de hoekpunten van een regelmatig viervlak. Moleculen natriumchloride, keukenzout dus, vormen kubusvormige kristallen. Ze vormden een van de eerste objecten die de Hollandse ontdekkers van de microscoop als 'kleine teerlingetjes' konden waarnemen wanneer zij een druppel zout water lieten verdampen. Grotere kristallen kan men in de zoutmijnen van Midden-Europa vinden als steenzout. Een heel eenvoudige stof als koolstof kan onder bijzondere omstandigheden achtvlakkige kristallen vormen, die we kennen als diamanten. Menigeen heeft in zijn jeugd kennisgemaakt met zulke vormen, soms door in een verzadigde oplossing van suiker of van aluin een kristal aan een neerhangend touwtje te laten ontstaan, of gewoon door te kijken naar de neerdwarrelende sneeuwvlokken (ﬁguur 1.11).
Een kristal is een ruimtelijke herhaling van eenzelfde elementaire bouwsteen. Een kristal, bijvoorbeeld een suikerkorrel, kan uit onvoorstelbaar veel identieke moleculen bestaan. Het molecuul was tot voor kort ontoegankelijk voor directe waarneming, maar aan een kristal kunnen uitvoerige metingen worden verricht, waarbij de resultaten ons iets vertellen over de structuur van het molecuul. Een kristal kunnen we opvatten als een uit stangetjes gevormd ruimtelijk rooster.
Wanneer we die constructie belichten met een bundel evenwijdige lichtstralen, hangt het van de richting af of de lichtstralen er doorheen gaan of door de spijltjes worden tegengehouden. Op het moleculaire niveau moeten we echter niet aan scherp begrensde lichtstralen denken, maar meer aan de breking van lichtgolven door enigszins vage barri`res. De belichting van een kristal met bijvoorbeeld een bundel röntgenstralen bewerkt op een fotograﬁsche plaat als projectie een zogenaamd diffractiepatroon. Het maken van dergelijke patronen is voor chemici een methode om de onbekende structuur van een gegeven chemische stof, hemoglobine bijvoorbeeld, te kunnen ontraadselen.
Symmetrie in de vorm van herhaling en regelmaat is niet alleen een zaak van schoonheid, maar is ook van wetenschappelijk nut. Kristallen zijn mooi en ze zijn nuttig. Diamant, opgebouwd uit een van de meest elementaire chemische stoffen, koolstof, wordt gekenmerkt door een uiterst hechte kristalstructuur. Zuiver en met een passende grootte is een diamant een kostbaar bezit, maar onzuiver en klein is het dankzij de uitzonderlijke hardheid van groot nut waar moet worden geboord en geslepen. Dat ook van een zuiver chemisch onderzoek als röntgendiffractie inspiratie kan uitgaan voor de toegepaste kunst, bewijst ﬁguur 1.12, waarin huishoudelijk textiel als decoratie met diffractiepatronen is bedrukt. Aan het begin van de jaren vijftig was het tijdens het Festival of Britain in Londen te koop.

Met de moderne technische hulpmiddelen heeft men van een kristalvlak een soort microfoto kunnen maken, waarbij de moleculaire structuur zichtbaar wordt. In ﬁguur 1.13 laten we een deel van het oppervlak zien van een enkel siliciumkristal, het materiaal voor de kern van het hedendaagse rekentuig. De afbeelding is ontleend aan het IBM Journal of Research and Development van 1986.
Het valt op dat de kristallen in de natuur alle zijn gebaseerd op de getallen 3, 4 en 6. Het getal 5 lijkt niet voor te komen. Die constatering kan langs wiskundige weg gemakkelijk worden bewezen. Het is niet mogelijk een zich herhalende regelmatige ruimtelijke structuur te vormen waarin een vijftallige symmetrie voorkomt. Toch blijken er chemische stoffen te bestaan die zich niet aan deze verbodsregel schijnen te houden. Dat fenomeen is pas kort geleden opgehelderd, toen Roger Penrose ontdekte dat het mogelijk was een plat vlak volledig te bedekken met slechts twee soorten tegels, die waren afgeleid van een regelmatige vijfhoek. De met de tegels van Penrose te vormen tegelvloeren zijn ook niet echt regelmatig in de zin dat eenzelfde patroon zich exact in alle richtingen op dezelfde wijze herhaalt, maar veel scheelt het niet.
Men kan dat fenomeen vergelijken met de structuur van meetbare en onmeetbare getallen. Een meetbaar getal (gemakshalve tussen 0 en 1 gekozen) is per deﬁnitie een niet te vereenvoudigen breuk m/n, waarbij m en n natuurlijke getallen zijn. Proberen we een dergelijk getal te schrijven als een decimale breuk, dan blijkt de ontwikkeling van decimalen of af te breken, of uit te lopen op de exacte herhaling van een zelfde groepje getallen. Een eenvoudig voorbeeld: 3/7 = 0,428571 428571 428571... Daartegenover staan de zogenaamde onmeetbare getallen als √2, pi en e, het grondtal van het natuurlijke logaritmenstelsel. De decimale ontwikkeling van een onmeetbaar getal is een oneindige rij getallen zonder een zich herhalend patroon.

De symmetrie van de levende natuur
Aan de in de natuur voorkomende symmetrische vormen zou een apart boek kunnen worden gewijd. Het onderwerp is zo veelomvattend, dat we ons hier tot een enkele opmerking moeten beperken. Wat opvalt is dat de mooiste of rijkste symmetrievormen worden aangetroffen bij de eenvoudigste levensvormen. Wij mensen hebben uiterlijk alleen een spiegelsymmetrie, maar inwendig is de symmetrie gebroken, omdat we slechts een enkel, normaal links geplaatst, hart bezitten. Bij zeesterren treffen we echter een rotatiesymmetrie aan, evenals bij vele andere zeebewoners. Bij kwallen denken velen aan akelige prikken of aan vormloze hoopjes glibber op het strand. Maar wie ze in het water ziet zweven, in een natuurdocumentaire met fotograﬁsche hoogstandjes, weet wel beter.
Ooit waren Boheemse glaskunstenaars gefascineerd door hun wondere schoonheid. Aan het eind van de vorige eeuw wisten twee glasblazers, vader en zoon, de natuur te evenaren met gelijke wonderen van glasblazerskunst. Onlangs waren ze te zien in het glasmuseum te Leerdam. Twee fraaie objecten reproduceren we in ﬁguur 1.14.

1.16 Een diatomee

Een soortgelijke draaiingssymmetrie zien we in de plantenwereld. Een orchidee heeft slechts een spiegelsymmetrie, maar bij bloemen als de lelieachtigen komt de draaiingssymmetrie aan bod. Reeds met eenvoudige computerprogramma's kunnen we mathematische bloemvormen simuleren; ze heten dan soms fractals. Maar met echte bloemen hebben ze de symmetrievorm en de kleurenpracht gemeen. In ﬁguur 1.15 in het kleurkatern zien we daarvan een enkel voorbeeld.
Met programma's van de diskette kunnen nog veel meer kleurige bloemen geplukt worden.

De microscopische wezentjes die wij diatomeeën noemen, waarvan de kalkskeletjes lagen van krijtsteen hebben gevormd, laten fraaie vormen van ruimtelijke symmetrie zien. In hoofdstuk 6, wanneer we de vijf regelmatige lichamen bespreken, komen we er nader op terug. Hier beperken we ons tot de afbeelding van een enkele diatomee (ﬁguur 1.16).
terug naar de Inhoud

5. De tegels van Penrose
In het vorige hoofdstuk hebben we ons beziggehouden met regelmatige verdelingen van het platte vlak, een soort kristallografie van twee dimensies. In het bijzonder hebben we gekeken naar tegelpatronen waarbij met een beperkt aantal tegeltypen het gehele vlak op regelmatige wijze bedekt kon worden. De daarbij optredende symmetrieën zijn de translatie in twee richtingen, de zogenaamde herhalingssymmetrie, rotatiesymmetrie en spiegelsymmetrie. De rotatiesymmetrie kan slechts van de orde 2, 3, 4 of 6 zijn. Een vijftallige symmetrie is niet mogelijk.
Regelmatige tegelpatronen worden gekenmerkt door periodiciteit in twee richtingen waarbij eenzelfde element op identieke wijze almaar wordt herhaald. De meest eenvoudige betegeling is een overdekking van het vlak door parallellogrammen. Door de basistegel, een parallellogram, een bijzondere vorm te geven, kunnen tegelpatronen met meer symmetrieën ontstaan. Men heeft zich al lang geleden de vraag gesteld of het mogelijk was het vlak ook op een nietperiodieke wijze met tegels te bedekken, liefst met een of twee tegeltypen. Ruim vijftig jaar geleden vond Heinz Voderberg al een spiraalvormig patroon waarbij slechts een enkele tegel, een negenhoek, werd gebruikt. Dit was het begin van een reeks ontdekkingen die althans in meetkundige zin haar voorlopig einde heeft gevonden in de ontdekking van Roger Penrose van zeer bijzondere aperiodieke tegelpatronen met een vijftallige rotatiesymmetrie.

Spiraal en sfinx
In 1955 liet Michael Goldberg zien dat op uiterst eenvoudige wijze spiraalvormige tegelpatronen gevormd konden worden. In ﬁguur 5.1 zien we een tamelijk eenvoudige stervormige betegeling, opgebouwd uit gelijkbenige driehoeken met een tophoek van datrtig graden. De ﬁguur is natuurlijk niet periodiek, maar bezit wel een twaalftallige rotatiesymmetrie. Wanneer we met Goldberg de onderste helft van dat ﬁguur een stap naar rechts verschuiven, ontstaat een nieuwe ﬁguur, een spiraalvormig patroon van driehoeken dar voortgezet het gehele vlak overdekt (figuur 5.2). Een ander hekend voorbeeld is de sfinx van Solomon Golomb, een regel waarmee een spiraalvormige overdekking van her hele vlak mogelijk is. De sﬁnxregel is aan weerszijden te gebruiken, en met vier exemplaren als getoond in ﬁguur 5.3 kan een grotere sfinx worden gevormd. Kennelijk kunnen we dit zien als de eerste stap van een oneindige reeks waarbij uit vier exemplaren relkens weer een grotere gelijkvormige sfinx kan worden opgebouwd.

De gulden snede
Het blijkt dat bij de meest interessante niet-periodieke regelpatronen het getal 5 en de gulden-snedeverhouding opduiken. Vooruitlopend op latere beschouwingen, vatten we het voornaamste hier even samen. Het zogenaamde gulden-snedegetal (-1+√5)/2 is in de wiskunde een van de interessantste (onmeetbare) getallen. In een zekere volgorde van belangrijkheid komt het meteen achter pi en e, het grondtal van het natuurlijke logaritmestelsel. In dit hoofdstuk noteren we het gulden-snedegetal als a, de numerieke waarde is ongeveer 0,618.
De eigenschappen van dat getal kunnen we op meetkundige wijze weergeven, zoals in de ﬁguren 5.4 en 5.5. In het eerste plaatje zien we een liggende rechthoek (de gulden rechthoek) waarvan de horizontale zijde gelijk is aan 1, de meeteenheid. Van die rechthoek verwijderen we een vierkant en we houden nu een kleinere staande rechthoek over die gelijkvormig is met de grote rechthoek. Gelijkstelling van de verhouding van de rechthoekszijden geeft: a : (1 - a) = 1 : a
Hieruit volgt dat a² + a - 1 = 0, een vierkantsvergelijking waaruit meteen a = (-1+√5)/2 volgt. In de ﬁguur is die meetkundige bewerking enige malen herhaald, wat resulteert in een reeks van vierkanten die onbepaald kan worden voortgezet.

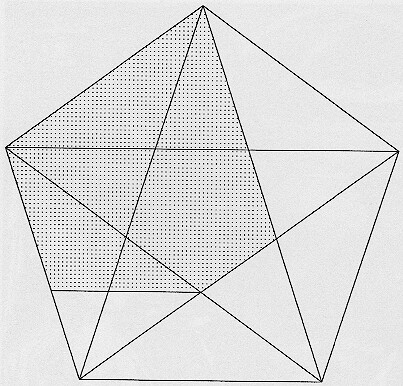
In ﬁguur 5.5 zien we een staande gelijkbenige driehoek met een tophoek van 36 graden, de basishoeken zijn dus elk 72 graden (de gulden driehoek). We kunnen constateren dat de bissectrice van een van de basishoeken van de grote driehoek een verkleinde gelijkvormige versie afsnijdt. Is 1 de lengte van de opstaande zijde en a de lengte van de basis, dan is de basis van de kleinere driehoek gelijk aan a². Uit de ﬁguur kunnen we aﬁezen dat a = 1 - a², weer dezelfde vierkantsvergelijking als zoëven.
De verhouding a van basis en opstaande zijde is dus de 'golden ratio', de gulden snede. In ﬁguur 5.6 is een regelmatige vijfhoek getekend met zijn diagonalen, die zelf een pentagram vormen. De ﬁguur is kennelijk opgebouwd uit de elementen van ﬁguur 5.5, en we komen aldus tot de condusie dat de diagonalen van een regelmatige vijfhoek elkaar snijden volgens de gulden-snedeverhouding.

Roger Penrose
De Engelse fysieus en wiskundige Roger Penrose was in 1954 tijdens een internationaal wiskundig congres te Amsterdam in contact gekomen met het graﬁsche werk van Maurits Escher. In dat jaar hadden de organisatoren van dat congres in het Stedelijk Museum te Amsterdam een tentoonstelling georganiseerd waar de aandacht werd gevestigd op de beroemde, maar toen nog weinig bekende Nederlandse graﬁcus. De wiskundigen waren geboeid door de regelmatige patronen van vogels, vissen en paarden en door Eschers experimenten met ruimtelijke projecties. Penrose zou Escher later inspireren tot zijn 'onmogelijke' ﬁguren op het thema van de driebalk, door Escher verwerkt tot een waterval en een oneindige wenteltrap.
In ﬁguur 5.7 zien we een computerversie van een dergelijke trap. Men kan fantaseren dat een lotgenoot van Sisyphus in de Griekse onderwereld was veroordeeld, onder het gewieht van een zware last, tot het beklimmen van een dergelijke trap. Ontvluchten was er niet bij, want in afdalende richting schoot hij evenmin op. De ﬁguur is tegelijk een manier om een ringvormig deel van een vlak te betegelen.
Penrose hield zich eveneens bezig met het probleem het vlak op niet-periodieke wijze te overdekken met tegels van een beperkt type. In 1973 slaagde hij daarin met een serie van zes tegeltypen, een mooi resultaat. Eenmaal op de goede weg wist hij het aantal typen te reduceren tot vier, en een jaar later, in 1974, zelfs tot twee. Penrose had ook iets van een zakenman in zich, en hij zag het belang van zijn vondst in voor het ontwerpen van commerciële puzzels. Hij vroeg dus patenten aan in de Verenigde Staten, Japan en natuurlijk Engeland. In het januarinummer van Scientiﬁc American van 1977 maakte Martin Gardner, de bekende columnist van 'mathematieal recreations', de legpuzzel wereldkundig.

Vlieger en pijl
De genoemde twee tegels van Penrose zijn afgebeeld in ﬁguur 5.8. In ﬁguur 5.9 zien we dat ze kunnen worden opgevat als delen van een ruit. Hun vorm doet denken aan een vlieger en aan een pijlpunt, en in de Engelstalige literatuur worden ze dan ook kite en dart genoemd, benamingen die we hier in technische zin gemakshalve overnemen.
De hoeken van de driehoeken waarin de ruit als in ﬁguur 5.9 verdeeld is, zijn veelvouden van 36 graden. De driehoeksvormen van ﬁguur 5.5 vinden we erin terug. De lengten van de zijden van kite en dart zijn dus 1 voor een lange zijde en a, het guldensnedegetal, voor een korte zijde.

De tegels van Penrose kunnen als bouwstenen van een legpuzzel op verschillende wijzen aan elkaar gepast worden. Het eenvoudigste is natuurlijk om ze zoals in ﬁguur 5.9 tot een ruit aan elkaar te passen, maar dat geeft geen nieuw gezichtspunt.
Met alleen ruiten kan een tegelvloer worden gelegd, maar dat patroon is zo regelmatig en zo weinig boeiend, dat Penrose er aanleiding in zag deze wijze van samenvoeging te verbieden. Hij zocht naar een eenvoudige regel om de tegelzetter als het ware te dwingen onregelmatige en verrassende ongewone patronen te leggen. In de praktijk kan zo'n regel op verschillende manieren technisch uitgewerkt worden. Hier volgen we de eenvoudige conventie dat we de hoekpunten van kite en dart hetzij met de kleuren rood en groen, of als cirkel en vierkant markeren. Bij het aan elkaar voegen dient dan tevens de kleur of de vorm overeen te stemmen. In ﬁguur 5.10 zien we een voorbeeld van het gebruik van een markering. De kite is gemarkeerd met vierkantjes op de hoekpunten op de symmetrieas. De dart heeft dezelfde markering daarentegen op de vleugeltips. Een eenvoudige consequentie is dat de twee vormen nooit tot een ruit mogen worden verenigd.
In de ﬁguren 5.11 en 5.12 laten we zien hoe met een paar tegels al interessante ﬁguren kunnen worden gevormd. In zekere zin zijn het bouwstenen van een hogere orde, herkenbare elementen in tal van Penrose-patronen, ﬁguren die ook een eigen naam hebben gekregen als ace, king, queen, jack enzovoort. Ook hier behouden we de Engelse naamgeving. Er zijn precies zeven manieren waarop de tegels op cirkelvormige wijze om een centraal punt kunnen worden gelegd. Men kan dat vrij gemakkelijk zelf narekenen, wanneer men bedenkt dat de volle hoek van 360 graden moet worden verdeeld in stukken van 36, 72 (de hoeken van de gulden driehoek) en 144 graden.

Inflatie en deflatie
Er bestaat een heel interessante manier om op systematische wijze uit een bestaand Penrose-patroon een ander patroon af te leiden. Het is mogelijk een gegeven patroon af te breken door op een bepaalde wijze tegels aan elkaar te lassen tot nieuwe tegels, een tamelijk ingewikkeld proces waarbij ook halve tegels zijn betrokken. Deze methode, inflatie genaamd, kan vele malen achter elkaar worden uitgevoerd. Bij elke stap worden de tegels groter, maar wanneer het patroon zich oneindig ver uitstrekt, heeft dat geen verdere consequenties. Wanneer we beginnen met een patroon dat uit eindig veel tegels bestaat, wordt het totale aantal door het inﬂatieproces gereduceerd totdat we slechts een paar tegels overhouden. Bij het omgekeerdat proces, de deﬂatie, worden steeds meer tegels gevormd. Bij elke deflatiestap vindt zowel een vermeerdering van tegels plaats als een verkleining van afmetingen, maar uiteraard kunnen we de verkleining compenseren tot een schaalvergroting.
Het proces van deﬂatie kan met behulp van de computer vrij gemakkelijk worden gesimuleerd en op deze wijze kunnen uit een enkele tegel of een van de modellen van de ﬁguren 5.11 en 5.12 systematisch meer uitgebreide patronen worden afgeleid. De techniek van de inﬂatie en de deflatie is uitvoerig besproken in het mooie boek van Grünbaum en Shephard, Tiling and Patterns. Hier volstaan we met de meetkundige toelichting van de ﬁguren 5.13 en 5.14.
De kite wordt bij de deﬂatie aangevuld met twee halve tegels, waardoor de omtrek van de nieuwe ﬁguur ontstaat. Daarin is plaats voor vier kleinere kites en twee kleinere darts als aangegeven in de ﬁguur. Wanneer de deﬂatie op twee aangrenzende tegels wordt toegepast, treedt een overlap op die niet storend is. Het komt erop neer dat bij een strikte opvolging van de deflatieregel twee tegels op dezelfde plaats terechtkomen. In ﬁguur 5.14 wordt op analoge wijze uit een dart een nieuwe ﬁguur van drie kites en twee darts afgeleid.
In de ﬁguren 5.15, 5.16, 5.17 en 5.18 is de deﬂatie toegepast op het zonnemotief van vijf kites. In ﬁguur 5.15 zien we het resultaat na een enkele deflatiestap. Het centrum is vervangen door een ster, terwijl de ﬁguur uitgebreid is met een rand van tien kites. Het resultaat van een volgende deﬂatie wordt getoond in ﬁguur 5.16. In het centrum is de sun weer teruggekeerd en het totaal aantal tegels is aangegroeid tot 35 kites en twintig darts, 55 in totaal. De volgende stap geeft een patroon van 110 kites en 65 darts, zoals afgebeeld in ﬁguur 5.17. Ten slotte geeft de vierde fase een patroon met 315 kites en 19o darts (ﬁguur 5.18).
Alle patronen hebben een perfecte vijfvoudige rotatiesymmetrie, de diëdergroep D5. In al deze patronen kan men de typen van de ﬁguren 5.11 en 5.12 terugvinden, in het bijzonder de sun, star en de ace. De hier gegeven patronen zijn verkregen met behulp van een computerprogramma dat gebruik maakt van de zogenaamde Lindenmayersystemen en de schildpadmethode. Programma en technische details kan men vinden op de diskette. Als extra bevinden zich in het kleurkatern een illustratie van de deflatie van de star, ﬁguur 5.19, en van de sun, ﬁguur 5.20.

De verboden vijf
We zijn nu zo'n twintig jaar verder en het belang van de tegels van Penrose is de speelgoedwinkel ver ontstegen. Het blijkt zelfs dat er in de natuur quasi-kristallijne structuren bestaan die we dankzij de theorie van Penrose nu beter kunnen begrijpen. Er bestaan kristallijne stoffen die in handen van fysici een vijftallige symmetrie vertonen. In 1984 ontdekten enkele Amerikaanse onderzoekers bij een legering van aluminium en mangaan zo'n merkwaardige stof. Een regelmatige periodieke moleculaire structuur van een kristal wordt onder andere zichtbaar wanneer men er licht van een bepaalde golﬂengte, bij voorkeur röntgenstralen, op laat vallen. De moleculaire bouw van de kristallijne materie doet de invallende lichtstralen op een zeer bepaalde manier afbuigen, en men verkrijgt daarbij een zogenaamd diffractiepatroon, een soort projectie van de moleculaire structuur die dezelfde symmetrie-eigenschappen bezit als de kristallijne stof.
In de kristallograﬁe kan men geen vijftallige rotatiesymmetrie krijgen, omdat die op meetkundige gronden strijdig is met de herhaalbaarheid van de kristalbouw. Des te groter was de verbazing van de fysici dat zij in een enkel, kennelijk zelden voorkomend, geval toch op een vijftallige symmetrie stuitten. Maar wijzer geworden door de legpuzzel van Penrose, kunnen we nu tot de volgende verklaring komen. Er bestaan (vlakke) quasi-regelmatige patronen waarin lokaal het getal 5 een essentiële rol speelt, meetkundig bestaat het patroon uit fragmenten van regelmatige vijfhoeken. Het patroon herhaalt zich weliswaar niet, maar brokken van het patroon treft men overal in nauwelijks ongewijzigde vorm aan. Men zou kunnen zeggen dat het patroon, afgezien van een statistische spreiding, globaal regelmatig is met een soort statistische vijftallige symmetrie. Het statistische karakter van de symmetrie blijkt ook uit de relatieve vaagheid van het diffractiepatroon. De zogenaamde resonantielijnen zijn niet zo scherp als bij de favoriete drietallige of viertallige symmetrie.
terug naar de Inhoud

6. De platonische lichamen
De Griekse wiskundigen van de klassieke oudheid kenden het bestaan van vijf regelmatige veelvlakken, meetkundige lichamen begrensd door regelmatige veelhoeken van dezelfde soort die in elk hoekpunt op dezelfde wijze bij elkaar komen. Iedereen kent natuurlijk de kubus uit de tijd dat hij als kleuter nog met de blokkendoos speelde. De Grieken spraken van een hexaëder, een woord dat is samengesteld uit het telwoord hex voor zes en hadron voor vlak. Veel van die Griekse termen worden nog steeds gebruikt, vooral in technische literatuur. In plaats van veelvlak zeggen we polyëder, met dezelfde betekenis.
Een paar eeuwen geleden spraken we in onze taal van een 'teerling' en konden we in een oud boek over microscopie lezen dat er bij het opdrogen van een druppel zout water kleine teerlingetjes te zien waren. Helaas is dat mooie Nederlandse woord in onbruik geraakt. Enkelen kennen het nog in de vertaling van de uitroep van Julius Caesar toen hij een politieke beslissing had genomen en de rivier de Rubicon overstak, zeggende: "De teerling is geworpen." Het woord 'teerling' is daarbij de vertaling van het Latijnse 'alea', met de betekenis van dobbelsteen. Nu spreken we wat deftiger van kubus en zeggen we bol, terwijl onze voorouders het woord kloot gebruikten.
De kubus is een van de eenvoudigste regelmatige veelvlak. We kunnen de kubus karakteriseren met de symbolische notatie {4,3}, wat wil zeggen dat er vier hoekpunten per zijvlak zijn en dat er in elk hoekpunt drie zijvlakken, en dus ook drie ribben, samenkomen. Een andere manier is om het aantal hoekpunren (H), ribben (R) en zijvlakken (Z) te vermelden. Dat geeft de notarie (8,12,6). Daarbij geldt als voor elk ander (gewoon) veelvlak de beroemde formule van Euler, die zegt clar het aantal ribben de som van de aantallen hoekpunten en zijvlakken met twee overtreft: H + Z = R + 2.

Het eenvoudigste regelmatige lichaam is de driezijdige piramide, waarbij de zijvlakken gelijkzijdige driehoeken zijn. De Griekse traditie volgend spreken we van een retraëder, een woord waarin we het Griekse telwoord voor vier herkennen. De wiskundige notaties zijn {3,3} en (4,6,4).

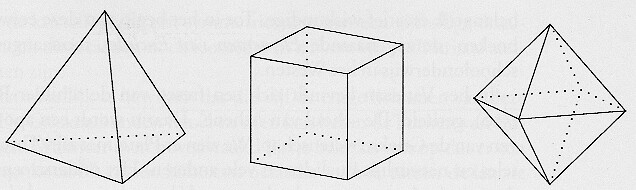
6.1 Viervlak, kubus en achtvlak
tetraëder, hexaëder, oktaëder

Het volgende regelmatige lichaam is een dubbele vierzijdige piramide, waarvan de acht zijvlakken weer gelijkzijdige driehoeken zijn, een oktaëder of eenvoudiger een regelmatig achtvlak. De notaties zijn {3,4} en (6,12,8). In ﬁguur 6.1 hebben we de drie eenvoudigste regelmatige lichamen afgebeeld volgens een parallelprojectie.
Overigens zullen we de toevoeging 'regelmatig' in dit hoofdsruk vaak weglaten omdat we, behoudens een enkele uitzondering, geen andere dan regelmatige veelhoeken en veelvlakken beschouwen. In het volgende hoofdstuk laten we iets van de regelmatigheid vallen en beschouwen we bijvoorbeeld veelvlakken waarbij de zijvlakken regelmatige veelhoeken van ongelijk type kunnen zijn. Een mooi voorbeeld is het model van een voetbal begrensd door twintig zeshoeken en twaalf vijfhoeken.

De school van Athene
Voor velen van ons zijn dit de enige bekende regelmatige veelvlakken. Maar wie op school het geluk heeft gehad de nodige meetkundige kennis op te doen, zal ook op de hoogte zijn van het bestaan van een regelmatig twaalfvlak en een regelmatig twintigvlak. Toch is het bepaald geen eenvoudige zaak om, zonder meetkundige uitrusting, het bestaan van dergelijke objecten te bewijzen. Het is daarom bijna verbijsterend te moeten ervaren dat de Griekse wiskundigen meer dan twintig eeuwen geleden volledig op de hoogte waren en, meer nog, ook konden bewijzen dat dit de enige vijf veelvlakken waren die het predikaat regelmatig mochten verwerven.
In de tijd van Pythagoras was het regelmatige twintigvlak of ikosaëder reeds ontdekt, maar was men nog onbekend met het regelmatige twaalfvlak of dodekaëder . Timaios van Locri, een der meest bekende Pythagoreeërs, zag een mystiek verband tussen de vier bekende regelmatige lichamen en de elementen vuur, lucht, water en aarde. Wel zag hij zich genoodzaakt zijn theorie aan te passen aan de ontdekking van het twaalfvlak in zijn tijd. Niet van zijn stuk te brengen, vatte hij de dodekaëder op als de vorm van het alles omspannende wereldruim.
De wiskundige Theaitetos van Athene gaf van alle vijf een beschrijving die is overgeleverd in een paar hoofdstukken van de geschriften van de ons beter bekende Eukleides (Eukleides, ca. 300 v.Chr.).
Plato (428-348 v.Chr.), steunend op de kennis van de school van Pythagoras, beschreef het vijftal in zijn bekende naar Timaios genoemde natuurﬁlosoﬁsche dialoog. Dat werk, dat een goed beeld geeft van de Griekse wereldbeschouwing, is tot in de renaissance toonaangevend geweest. Ook het verhaal van de ondergang van Atlantis, zoals we nu weten het gevolg van een historisch nauwkeurig te dateren aardbeving, is daarin vermeld. Het gezag van Plato was dermate hoog, dat men de vijf regelmatige lichamen nog tot in onze tijd als de platonische lichamen aanduidt. Ook de naam van Eukleides leeft op allerlei wijzen voort, maar we moeten daarbij wel bedenken dat hij eerder een begaafd schrijver en redacteur was dan een belangrijk creatief wiskundige.
Tot in het begin van deze eeuw waren zijn boeken, de zogenaamde Elementen van Eukleides, toonaangevend in het schoolonderwijs in het westen. In het Vaticaan bevindt zich een fresco van de schilder Rafaël (1483-1520), getiteld 'De school van Athene'. Daarin wordt een apotheose gegeven van de Griekse wetenschap. We zien er Plato met zijn Timaeus, Aristoteles en natuurlijk Euklides en vele anderen. Het onderstreept het belang dat men in de renaissance hechtte aan de bestudering van de kennis van de antieke wereld.

De platonische lichamen
Dodekaëder en ikosaëder zijn afgebeeld in ﬁguur 6.2. Hun belangrijkste eigenschappen en die van het eerste drietal verenigen we hieronder in een tabelletje.

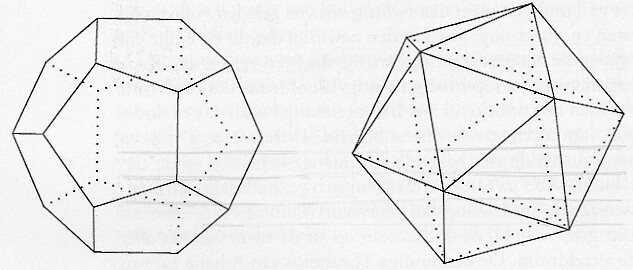
6.2 Twaalfvlak en twintigvlak
dodekaëder, ikosaëder

tetraëder	{3,3}	(4,6,4)
kubus	{4,3}	(8,12,6)
oktaëder	{3,4}	(6,12,8)
dodekaëder	{5,3}	(20,32,12)
ikosaëder	{3,5}	(12,32,12)

Het lijstje is hiermee compleet, tenminste wanneer we ons tot bolvormige, preciezer gezegd convexe, lichamen beperken. Laten we die eis vallen, dan kunnen ook regelmatige stervormige lichamen geconstrueerd worden met de symmetrie van dodekaëder en ikosaëder. In hoofdstuk 8 gaan we daar wat dieper op in. Bij wijze van voorproefje tonen we in ﬁguur 6.3 de grote ikosaëderster van Poinsot, en in ﬁguur 6.4 de grote dodekaëderster van dezelfde Franse geometer.

Het blijft gissen hoe de Grieken tot hun ontdekkingen zijn gekomen. Viervlak en kubus liggen wel erg voor de hand, het achtvlak zou afgeleid kunnen zijn uit een Egyptische piramide en haar weerspiegeling in het water. Ook zouden kristalvormen in de natuur aanleiding kunnen zijn tot het ontdekken van interessante regelmatige veelvlakken. Helaas verbieden de wetten van de kristallograﬁe een symmetrievorm met een vijftallige draaiing, zodat noch dodekaëder, noch ikosaëder in zuivere vorm als kristal aanwezig kunnen zijn.

Het is niet moeilijk te bewijzen dat die vijf de enige lichamen van deze soort zijn. De Grieken konden het al en men kan het in de boeken van Euklides nalezen. Wanneer men bovenstaand lijstje bekijkt, valt op dat er een zekere overeenkomst is tussen kubus en oktaëder en ook tussen de laatste twee regelmatige lichamen. Het is alsof vlakken en punten verwisseld zijn. Het is een manifestatie van een belangrijk principe in de ruimtelijke wiskunde, die wordt aangeduid als dualiteit of polariteit.
Uit een regelmatig lichaam kan de zogenaamde polaire ﬁguur worden afgeleid door de centra van de zijvlakken op te vatten als de hoekpunten van een veelvlak. Voeren we het uit voor een kubus, dan levert elk vierkant zijvlak een hoekpunt, in totaal dus zes, en die vormen met elkaar een regelmatige achtvlak. Omgekeerd kan uit een achtvlak weer een kubus worden afgeleid door de centra van de acht driehoekige zijvlakken als hoekpunten te nemen. Dezelfde methode werkt ook bij twintigvlak en twaalfvlak.

Bij elk regelmatig lichaam behoort een ingeschreven bol die aan alle zijvlakken raakt en een omgeschreven bol die door alle hoekpunten gaat. Eucklides wijdt er al de nodige aandacht aan en leert ons de straal van zulke bollen berekenen. Belangrijker voor ons is een soort middenbol die aan alle ribben raakt. Even een voorbeeldje: voor een kubus waarvan de coordinaten bepaald zijn door (±1,±1,±1) kan men gemakkelijk narekenen dat de straal van de ingeschreven bol gelijk is aan 1, de lengte van een halve ribbe, en dat de straal van de omgeschreven bol gelijk is aan √3. De straal van de middenbol is daarentegen √2.
De middenbol geeft aanleiding tot een andere uitwerking van het polariteitsprincipe. De polaire ﬁguur van een ribbe vinden we eenvoudig door de ribbe in zijn raakvlak aan de middenbol over een hoek van negentig graden te draaien. Eventueel moet de lengte van de gedraaide ribbe worden aangepast om bij de hoekpunten van het polaire veelvlak aansluiting te verzekeren.

De moderne school
Het is eigenlijk een wonder dat de leerboeken van Euklides tot aan het begin van deze eeuw praktisch ongewijzigd de enige leermethode waren tot het verwerven van met name meetkundige kennis. Sindsdien is het wiskunde-onderwijs sterk gemoderniseerd, en dat zal nog wel even zo blijven. Tegenwoordig is de wiskunde sterk op de utiliteit gericht, al zal niet alles wat men leert even nuttig blijken. Anderzijds zijn er stukken wiskunde als verstofte spullen op een rommelzolder weggegooid. Maar zoals een rommelzolder onverwachte, waardevolle antiquiteiten kan herbergen, zo zijn er stukken wiskunde in het onderwijs verdwenen die, hoewel niet zo erg nuttig, tot het culturele erfgoed mogen worden gerekend van onze westerse beschaving. We denken hierbij vooral aan platonische lichamen en aan de verwante objecten die in de volgende twee hoofdstukken ter sprake zullen komen. Overigens, veelvlakken kunnen wel degelijk tot een heel concrete toepassing leiden.
Hoe kunnen we een door veelhoeken begrensde voetbal construeren die de bolvorm zo goed mogelijk benadert? Onlangs werd er in de koolstofchemie een regelmatige structuur ontdekt met een netwerk van zestig koolstofatomen. Welk meetkundig lichaam komt daarvoor in aanmerking?
Wie zich met voetballen bezighoudt, eventueel met ondersreuning van de televisie, kent op de eerste vraag twee antwoorden. We komen daarop terug in het volgende hoofdstuk over de halfregelmatige lichamen. Ook de tweede vraag zal daar worden beantwoord.
Ongetwijfeld zal in het moderne schoolonderricht veel gebruik worden gemaakt van de computer. De computer stelt ons op geriefelijke wijze in staat kennis te nemen van allerlei meetkundige ﬁguren. Platonische en andere typen veelvlakken kunnen op verschillende wijzen op het beeldscherm al of niet gekleurd verschijnen. We kunnen ze in verschillende projecties waarnemen door ze te draaien of door er als het ware zelf omheen te lopen. Eenvoudiger blijft echter de primitieve methode om met schaar en lijmpot een regelmarig veelvlak samen te stellen uit een bouwplaat. Zoals we in ﬁguur 6.5 kunnen zien is het vrij eenvoudig om een twintigvlak in elkaar te zetten. De bouwplaat van een twaalfvlak, afgebeeld in ﬁguur 6.6, vereist wat meer knip- en plakwerk.

Ruimtelijke symmetrie
De symmetrische structuur van een platonisch veelvlak kan worden beschreven door te letten op de ruimrelijke draaiingen die het lichaam met zichzelf tot dekking brengen. Als voorbeeld nemen we de kubus. Een draaiing over een willekeurige hoek om de as die de centra van twee overstaande zijvlakken met elkaar verbindt, brengt de kubus in het algemeen in een andere stand. Is het een hoek van negentig graden, dan stemt de eindpositie overeen met de beginpositie. We zeggen dan dat die draaiing de kubus met zichzelf tot dekking brengt. Hetzelfde is het geval voor hoeken van 180 en 270 graden (of min negentig graden). De kleinste positieve hoek met deze eigenschap is negentig graden, en omdat negentig graden viermaal in 360 graden is bevat, spreken we van een viertallige rotarie-as. Wie bekend is met het in hoofdstuk 2 besproken begrip van een wiskundige groep, herkent hier de uit vier elementen bestaande rotatiegroep C4.
De symmetrische structuur van een symmetrisch veelvlak kan worden vertaald in de opsomming van alle rotatieassen. Bij de kubus zijn drie van zulke viertallige rotatieassen. Met elkaar zijn dat negen draaiingen. Maar ook een rotatie over een hoek van 120 graden om een lichaamsdiagonaal brengt de kubus met zichzelf tot dekking. Die diagonalen zijn dus drietallige rotatieassen. Omdat er vier van zulke diagonalen zijn, levert dat in totaal acht draaiingen op. Ten slotte zijn er nog tweetallige assen, de verbindingslijnen van overstaande ribben. Daarvan zijn er zes, zodat we nu in totaal over 23 draaiingen beschikken. Met de identieke transformatie of identiteit krijgen we aldus een groepstructuur van 24 elementen, die bekendstaat als de oktaëdergroep. Het zou ook de kubusgroep kunnen heten, maar omdat oktaëder en kubus precies dezelfde symmetrische structuur hebben, is het niet nodig twee verschillende benamingen te gebruiken. Om historische redenen is de naamgeving afgestemd op het achtvlak.
De symmetrieën van een kubus komen te voorschijn wanneer we het lichaam in een speciale kijkrichting op een vlak projecteren. Lopen de projectielijnen evenwijdig aan een lijn die twee overstaande ribben van de kubus verbindt, dan krijgen we, zoals in ﬁguur 6.7, slechts een tweetal staande rechthoeken te zien. Van de zes zijvlakken zijn er twee zichtbaar en twee geheel onzichtbaar. Van de resterende twee zijn door de bijzondere ligging slechts streepjes zichtbaar. Met een projectie in de richting van een lichaamsdiagonaal krijgen we een projectie met een drietallige rotatieas, drie ruiten in een gelijkzijdige zeshoek. De helft van het aantal zijvlakken is zichtbaar. De hoogste graad van symmetrie is aanwezig bij een projectie in de richting van een der ribben. Van het object is nu slechts een enkel zichtbaar vierkant overgebleven.
In ﬁguur 6.8 is hetzelfde programma uitgevoerd voor het achtvlak, en weer zijn alleen de zichtbare delen getekend. De oktaëdergroep is in zijn structuur identiek met de in hoofdstuk 2 besproken permutatiegroep P4, de verschikkingen van vier elementen. Meetkundig kunnen we dat inzien door de hoekpunten van een kubus te nummeren met de getallen 1, 2, 3 en 4, waarbij overstaande hoekpunten hetzelfde nummer krijgen.
De symmetrie van het viervlak is eenvoudiger. Er zijn daarbij twee typen rotatieassen, vier drietallige assen die telkens een hoekpunt met het middelpunt van het overstaande zijvlak verbinden, en drie tweetallige assen die de middens van overstaande ribben met elkaar verbinden. In totaal 4 * 2 + 3 * 1 + 1 of twaalf draaiingen, inclusief de identiteit.
Zoals kubus en oktaëder als polaire ﬁguren dezelfde symmetrieën hebben, behoort ook bij dodekaëder en ikosaëder een zelfde symmetriegroep. De naam is ikosaëdergroep en het aantal elementen is zestig. Gaan we bijvoorbeeld uit van een twintigvlak, dan kunnen we vaststellen dat de zes lichaamsdiagonalen vijftallige rotatieassen zijn met in totaal 4 * 6 = 24 echte draaiingen. De lijnen die de centra van overstaande zijvlakken verbinden, zijn drietallige assen met 10 * 2 = 20 draaiingen. Ten slotte leveren de middens van overstaande ribben vijftien tweetallige assen voor even zovele draaiingen. Het totaal van 59 geeft met de identiteit ten slotte het genoemde aantal van zestig elementen. Ook de ikosaëdergroep kan in verband worden gebracht met een permutatiegroep. De groep heeft namelijk dezelfde structuur als de even deelgroep van P5, dat wil zeggen de groep bestaande uit de even permutaties van vijf elementen, maar het zou te ver voeren er dieper op in te gaan.
De symmetrieën van twintigvlak en twaalfvlak kunnen zichtbaar worden gemaakt door de lichamen in een bijzondere richting te bekijken. In ﬁguur 6.9 geven we drie speciale projecties van een twintigvlak. Gaat de projectierichting door de middens van overstaande ribben, dan is er alleen een tweetallige rotatieas met symmetrietype D2. Van de twintig zijvlakken zijn er acht volledig zichtbaar en van de twaalfhoekpunten zien we er eveneens acht. Volgt de kijkrichting de middelpunten van overstaande driehoekige zijvlakken, dan ontstaat een ﬁguur begrensd door een regelmatige zeshoek met de D3-symmetrie. De helft van alle zijvlakken is zichtbaar en van de hoekpunten zijn er drie onzichtbaar. Met een lichaamsdiagonaal als lijn van projectie krijgen we een projectie met de hoogste graad van symmetrie, type D5. Weer is de helft van alle zijvlakken zichtbaar en slechts één hoekpunt is onzichtbaar.
Op overeenkomstige wijze zijn in ﬁguur 6.10 symmetrische projecties van een twaalfvlak gegeven.

Het kosmische mysterie van Kepler
De Grieken meenden dat God de wereld op meetkundige wijze had geordend. In overeenstemming hiermee trachtten Hipparchos en Ptolemaeus de bewegingen van de planeten, zon en maan tot cirkelvormen te herleiden. In het stelsel van Ptolemaeus was de aarde het middelpunt van het heelal en bewogen de toen bekende vijf planeten met zon en maan eromheen. Dat stelsel mocht zich lang verheugen in de gunst van de kerkelijke autoriteiten. De aarde als middelpunt van de kosmos, en Jeruzalem als middelpunt van een, liefst platte, aarde. Dit middeleeuwse wereldbeeld is door Dante in zijn Divina Commedia uitgebreid en realistisch beschreven.
Copernicus (1473-1543) maakte een eind aan het mooie sprookje door de zon in het middelpunt te plaatsen. In zijn grote werk De Revolutionibus Orbium Caelestium (Over de omwentelingen der hemellichamen), gereed in 1530, poneert hij zijn stellingen met een uitvoerige argumentatie, maar hij kon er niet toe besluiten zijn boek uit te geven. Pas enige jaren voor zijn dood wisten vrienden hem daartoe over te halen en de eerste exemplaren van zijn gedrukte werk bereikten hem op zijn sterfbed.
Johannes Kepler (1571-1630) bouwde voort op het werk van zijn grote voorganger en kwam ten slotte tot de formulering van de naar hem genoemde wetten. Daarmee werd het platonische wereldbeeld, waarbij de beweging van de hemellichamen uit cirkels was opgebouwd, een opvatting die door Copernicus nog was gehuldigd, definitief verlaten. De ideale banen waren dus kegelsneden en de zon stond in een brandpunt van een ellipsvormige planetenbaan.
Voordat het echter zover was, had Kepler al eerder andere, en voor ons heel vreemde, denkbeelden gekoesterd. Hij was dan ook sterk astrologisch geïnteresseerd en had soms de grootste moeite zijn moeder tegen aanklachten van hekserij te beschermen. Zo kwam hij in 1595 op het idee dat de structuur van het planetenstelsel in verband moest staan met het bestaan van vijf regelmatige veelvlakken en dat de opeenvolgende planeetsferen beschouwd konden worden als omgeschreven en ingeschreven bollen van die lichamen. Hij zette dat denkbeeld uiteen in een in 1596 verschenen werk als het 'mysterium cosmographicum'. De in ﬁguur 6.11 gegeven afbeelding is aan dat werk ontleend. Kepler meende met die conceptie diep in de geheimen van de schepper te zijn doorgedrongen. De zes bollen corresponderen met de banen van Saturnus, Jupiter, Mars, de aarde, Venus en Mercurius. In de afbeelding onderscheiden we van buiten naar binnen gaande kubus, tetraëder, dodekaëder, oktaëder en ikosaëder. Gelukkig voor Kepler waren de overige drie planeten Uranus, Neptunus en Pluto nog niet ontdekt. Dat zou nog twee eeuwen duren.

In de natuur
In de wereld van de levenloze stof is alleen plaats voor de drie eenvoudige platonische lichamen. We hebben al eerder gezien dat kristallen met een strikte vijftallige symmetrie hier kunnen bestaan. Een kristal dat de vorm heeft van een regelmatig twaalfvlak of een twintigvlak zal men helaas nooit kunnen aantreffen. Maar wat niet lukt in de levenloze natuur, kunnen levensvormen wel klaarspelen.
De Duitse natuuronderzoeker Ernst Haeckel (1834-1919) beschreef in zijn publikaties kiezelzuurskeletjes van radiolarii, straaldiertjes, microscopisch kleine wezentjes, levend op de bodem van de zee. In ﬁguur 6.12 is uit een van zijn werken, Kunstforme der Natur, een enkele pagina afgebeeld. In die afbeeldingen kan men gemakkelijk de symmetrische structuur van de platonische lichamen terugvinden.
Met de moderne technieken van de natuurkunde is het mogelijk gebleken de structuur van virussen te ontraadselen. We weten nu dat een virus in principe bestaat uit een kern, drager van het erfelijke materiaal, en een bolvormige bedekking van eiwitten. In een aantal gevallen vertonen de manteleiwitten een symmetrievorm die met die van dodekaëder en ikosaëder overeenkomt; de symmetrie dusvan de ikosaëdergroep. In ﬁguur 6.13 is daarvan een afbeelding gegeven.
terug naar de Inhoud

7. Halfregelmatige lichamen
In de Griekse oudheid kende men naast de vijf regelmatige lichamen ook een aantal andere veelvlakken met een hoge graad van regelmatigheid. De vijf platonische lichamen zijn gekenmerkt door de eigenschap dat zijvlakken regelmatige veelvlakken van hetzelfde type zijn, waarvan er in elk hoekpunt evenveel tezamen komen. Men zou de eis kunnen laten vallen dat de zijvlakken regelmatige veelhoeken zijn.
Een andere mogelijkheid is om twee of meer regelmatige veelhoeken als zijvlak toe te laten. Die laatste mogelijkheid is door Archimedes onderzocht en de door hem beschreven serie halfregelmatige veelvlakken staat tegenwoordig bekend als de archimedische lichamen. Er zijn ook nog andere manieren om min of meer regelmatige lichamen te vormen, maar het zou in het bestek van dit boek te ver voeren al die mogelijkheden systematisch na te gaan. Van de archimedische veelvlakken, dertien in getal, zal wel een volledige tabellarische beschrijving worden gegeven, maar in het algemeen beperken we ons tot een keuze op grond van onder andere historische overwegingen.

Dürers 'melencolia'

7.1 'Melencolia' van Albrecht Dürer

De beroemde Duitse schilder Albrecht Dürer heeft zich uitvoerig met de meetkunde bemoeid en in het bijzonder met de theorie van het meetkundige perspectief. Hij schreef er zelfs een bekend leerboek over ten dienste van generaties schilders na hem. In zijn gravure getiteld 'Melencolia' (1514), afgebeeld in ﬁguur 7.1, laat hij een ander aspect van zijn meetkundige kennis zien. Een gevleugelde engel zit peinzend naast een meetkundig veelvlak dat doet denken aan een halfregelmatig lichaam. Verder zien we op de prent een tovervierkant, een schikking van getallen waarbij de som van de getallen van dezelfde rij of kolom steeds dezelfde uitkomst geeft. De prent is gedacht als één uit een serie van vier, overeenkomende met de vier temperamenten.
De beroemde Romeinse geneesheer Claudius Galenus (130-210) onderscheidde bij de mens vier verschillende lichaamssappen: bloed, slijm, gele gal en zwarte gal. Menging van die sappen leidde volgens hem tot een temperament dat hij sanguinisch, flegmatisch, cholerisch en melancholisch noemde. Die termen kennen we tegenwoordig ook, al zijn de opvattingen van Galenus allang verlaten. Bij melancholisch denken we aan zwaarmoedigheid, maar in de middeleeuwen werd het melancholische temperament met andere menselijke activiteiten geassocieerd: met werenschap en onderzoek bijvoorbeeld. Bij de gravure van Dürer moeten we dan ook eerder denken aan een eerbetoon jegens de wetenschap, aan wiskundige kennis van meetkunde en rekenkunde.

Het is de moeite waard het veelvlak iets nader te analyseren. Blijkbaar is het afgeleid van een parallellepipedum, een scheef blok begrensd door zes ruitvormige zijvlakken. Maar ook zien we dat het blok kennelijk afgeknot is. We zien dat bij een van de ruitvormige zijvlakken een driehoek afgesneden is door een snijlijn die evenwijdig aan een diagonaal van de ruit loopt. Het vermoeden ligt voor de hand dat de ﬁguur iets te maken heeft met de gulden-snedeverhouding.

7.2 De door Dürer gekozen vijfhoek

In ﬁguur 7.2 is nog eens de bekende ﬁguur van een regelmatige vijfhoek en het inwendig beschreven pentagram getekend. De ﬁguur bevat een aantal ruiten, elk bestaande uit twee zijden van de vijfhoek en twee delen van diagonalen, en we mogen aannemen dat zij de zijvlakken vormen van het nog niet afgeknotte veelvlak van Dürer. Wanneer we de afknotting uitvoeren met de in ﬁguur 7.2 getekende hulplijn, wordt een gulden-snedeverdeling tot stand gebracht en wordt een vijfhoek gevormd als bouwelement van het afgeknotte lichaam van Dürer. Aldus wordt het afgebeelde veelvlak begrensd door zes van die vijfhoeken en door twee gelijkzijdige driehoeken. De hoeken van de vijfhoeken zijn 72, 108, 126, 126 en 108 graden.
De kristallografe C.H. MacGillavry heeft in een publikatie in 1981 uitvoerig aandacht besteed aan het afgebeelde veelvlak. Daarbij zijn ook andere hypothesen naar voren gebracht en ook is de mogelijkheid uitgesproken dat Dürer zich heeft laten inspireren door een calcietkristal.
terug naar de Inhoud

terug naar het literatuuroverzicht

terug naar het weblog

^