Irrationele getallen: een aanwijzing voor Gods eeuwige oneindigheid
Inhoud
1. De getaltheorie en algebra
De eeuwigdurende werkzaamheid
2. De getaltheorie en meetkunde
De wiskundige uitbeelding van Jezus' leer
3. Het getal φ phi van de gulden snede
De verhouding tussen de mens, de heilige geest en de algeest
1. De getaltheorie in de algebra (van Arabisch 'al jebre': rekenen, rekenkunde)
Getalstelsels zijn door mensen ontwikkeld - dat wil zeggen: door de menselijke geest - want in de natuur zijn getallen als zodanig niet herkenbaar; zij zijn namelijk verborgen in natuurkundige formules, die een wiskundige weergave zijn van bepaalde natuurlijke gebeurtenissen. Het woord 'getal' hangt samen met 'tellen' en tellen is waarschijnlijk begonnen met de handen; er zijn nog steeds natuurvolken die slechts kunnen tellen op de vingers van één hand; alles wat daarna komt, wordt door hen 'veel' genoemd.
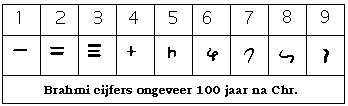De cijfers zoals wij die kennen, zijn door Indiase wiskundigen in de laatste eeuwen vóór Christus ontwikkeld: de z.g.n. 'brahmi-cijfers'. Let op het getal vier, dat de vorm heeft van het gelijkbenige kruis, dat verderop nog ter sprake komt (bron afbeelding: math4all.nl).Getallen worden als volgt ingedeeld:
| 1. Reële getallen: | a. Rationale getallen: natuurlijke getallen en breuken (ook repeterende breuken) |
| b. Irrationale getallen (een aantal daarvan zijn de transcendente getallen) | |
| 2. Irreële getallen: | imaginaire, complexe getallen uit de hogere wiskunde |
De reële en irreële getallen
Het woord 'reëel' is afgeleid van het Latijnse 're', dat 'ding' betekent, dus een 'voorwerp' dat tast- en zichtbaar is, in gedachten voorstelbaar en met lineaal en passer te tekenen.
Het woord 'ding' hangt samen met 'dingen' (van 'geding': een rechtszaak voeren) en met 'denken': in een rechtszaak moet over een (vaak gestolen) 'ding' worden 'gedacht', er moet een oordeel over worden 'bedacht'. Iets, wat een 'ding' is, kan men zich daardoor 'indenken', 'voorstellen'. Van een 'ding', van iets wat 'reëel' is, kun je je in gedachten een voorstelling maken, wat niet het geval is met iets, wat 'irreëel' is.
1. Ook bij getallen is er sprake van reëel en irreëel. De reële, natuurlijke getallen zijn de cijfers 0 t/m 9. Reële getallen zijn getallen, waarvan je je een voorstelling kunt maken, bijvoorbeeld van een aantal dingen of van een bepaald aantal punten, die samen een rechte lijn vormen, met een duidelijk begin en een duidelijk einde; bijvoorbeeld vijf punten die een rechte lijn, een zogenaamde getallenlijn, vormen: ・・・・・
Met de reële getallen kan op de gebruikelijke manier worden gerekend, zoals: optellen en aftrekken, vermenigvuldigen en delen.
2. Met de irreële getallen is dat echter heel anders. Zij behoren tot de hogere wiskunde en hebben de letter i van 'imaginair' gekregen, omdat zij denkbeeldig zijn en tot de 'complexe getallen' leiden. Van iets, wat 'irreëel' is, wat onwerkelijk of onwezenlijk is, kun je je nauwelijks een voorstelling maken; het kan uitsluitend 'in gedachten' van deskundigen bestaan, die geleerd hebben ermee te rekenen.
De rationale en irrationale getallen (de gebruikelijke, wiskundige termen, zijn germanismen)
a. De reële getallen kunnen rationaal of irrationaal zijn. De rationale getallen zijn getallen die een bepaalde 'ratio' of 'verhouding' tot elkaar kunnen hebben, zoals breuken.
Van bepaalde breuken kun je je nog wel een voorstelling maken, bijvoorbeeld van een halve punt (½) of van een kwart punt (¼) en ook de uitkomsten (quotiënt) van deze breuken: 0,5 en 0,25 behoren tot het voorstelbare.
b. Er zijn echter breuken van reële getallen, waarvan de uitkomst niet is op te schrijven, doordat er aan de uitkomst van de deling géén einde komt; daardoor is er ook geen voorstelling van te maken en worden zij daarom: de irrationale getallen genoemd (het voorvoegsel 'ir-' komt van het Latijnse voorvoegsel 'in-' of 'ir-' dat 'niet' of 'zonder' betekent; dus iets, wat niet rationeel is, oftewel niet gebaseerd op logica of reden en wat in dit verband betekent: schijnbaar rationeel, want een verhouding, maar toch ook weer niet, want... onoplosbaar).
Bekende voorbeelden van zulke irrationale getallen zijn:
√2 en √5, de vierkantswortels uit 2 en 5;
φ, het getal phi als verhouding van de gulden snede, die met de rij van Fibonacci samenhangt;
π, het getal pi, dat de verhouding tussen doorsnede (diameter) en omtrek van een cirkel weergeeft
en e, het grondtal van de natuurlijke logaritmes.
Beide laatste getallen zijn irrationaal en 'transcendent'.
De irrationale getallen π en e, die ook transcendent zijn
Het woord 'transcendent' komt van het Latijnse 'trans-scendere': overschrijden, een grens overgaan en in dit geval ook: ónbegrensd.
Een irrationaal, transcendent getal is een breuk met oneindig (∞) veel cijfers achter de komma (zonder dat er een patroon van zich herhalende cijfers optreedt); de decimalen van hun breuken overschrijden de grens tussen het zichtbare en onzichtbare, hun delingen gaan eeuwig door tot in het oneindig kleine: er komt nooit een einde aan, zij zijn eindeloos: een 'eeuwige oneindigheid'.
De gehele, natuurlijke getallen, 0 t/m 9, kent iedereen, maar sommige verschijnselen kunnen hiermee niet worden beschreven, daar zijn transcendente getallen voor nodig.
Het bekendste transcendente getal is π pi, dat de verhouding tussen de omtrek en doorsnede van een cirkel weergeeft. De benaderende waarde ervan is de breuk 22/7; π = 3,1415... → ∞ (gaat door tot in het oneindige), d.w.z. het getal π zelf is niet oneindig, want de waarde ervan ligt tussen 3,14 en 3,15 op de getallenlijn, maar het getal π heeft een oneindig aantal decimalen achter de komma en is daardoor onbepaald, en kan alleen worden benaderd, geschat.
Dat betekent dat je met een passer wel een zichtbare cirkel kunt trekken, maar dat de wáárde van dat lijnstuk in feite onbepaald blijft. Als je toch besluit die waarde uit te gaan rekenen (2π.r of π.diameter), dan blijf je eeuwig doorrekenen doordat je eerst de waarde van π moet bepalen. Datzelfde geldt voor het oppervlak: πr².
Het getal π is dus onbepaalbaar, een oneindigheid, maar toch komt het voor in meerdere natuurkundige formules, zoals in de Schrödingervergelijking, waarop de kwantumfysica berust.
Een tweede getal is e, het grondtal van natuurlijke logaritmes: e = 2,7182... → ∞.
Transcendente getallen zijn als deling van een verhouding, van een breuk te berekenen als een oneindige reeks getallen. Hoe langer je rekent (deelt), hoe nauwkeuriger het getal wordt, maar, daar kun je eeuwig mee doorgaan ... de reeks getallen verliest zich in de verten van de eeuwige oneindigheid! Het aantal transcendente getallen is zogenaamd 'overaftelbaar oneindig', wat betekent dat er meer transcendente getallen zijn dan gehele getallen.
Irrationale getallen
De breuken die leiden tot de irrationale getallen gaan in hun deling net als de transcendente ook door tot in het oneindige, maar hebben in die reeks getallen zich herhalende gedeeltes.
Voorbeelden: √2 en √5, de vierkantswortels uit 2 en 5.
Wortel 2 of √2 kan worden benaderd met de breuk 99/70, in decimalen 1,4142... → ∞.
Wortel 5 of √5 kan worden benaderd met de breuk 161/72, in decimalen 2,23611... → ∞.
Het getal φ phi als de verhouding van de gulden snede, die met de rij van Fibonacci samenhangt.
Volgens de Griekse wiskundige Euklides (Alexandrië, 4e eeuw v.Chr.) is de gulden snede de verdeling van een lijnstuk in 'de uiterste en middelste reden', oftewel een zodanige verdeling van een lijn, dat het grootste deel (a) zich verhoudt tot het kleinste deel (b) als hun beider geheel (a+b) tot het grootste deel (a) of a:b = (a+b):a.
Je kunt ook zeggen: het kleinste deel (b) verhoudt zich tot het grootste deel (a) als het grootste deel (a) zich verhoudt tot hun beider geheel (a+b, dat is: b:a = a:(a+b).
De verhouding a:b wordt het 'gulden getal' of φ phi genoemd. Dit invullen in de eerste verhouding geeft:
φ = 1 + 1/φ; met φ vermenigvuldigen leidt tot φ² = φ + 1 en vervolgens φ² - φ - 1 = 0
Dit is een vierkantsvergelijking; de positieve oplossing ervan is
Φ = (1 + √5)/2 = 1,6180... → ∞,
de negatieve oplossing φ is 0,6180... → ∞.
Eeuwigdurende werkzaamheid
Al deze irrationale getallen liggen gewoon op de getallenlijn, tussen de andere getallen, maar hun bestaan is in feite onvoorstelbaar door de eigenschap, dat ze als deling in het oneindig kleine nooit eindigen, maar eeuwig steeds maar weer bij iedere volgende deling een steeds kleiner wordend beetje toenemen. Het is een eeuwigdurende werkzaamheid, m.a.w. dit wiskundige feit verwijst naar de eeuwig durende werkzaamheid van de geest met zijn geestelijke vermogens.
Dit is een verschijnsel dat weliswaar in de natuur bestaat, maar daar niet kan worden opgemerkt. Het is een verborgen eigenschap, die alleen door het denken binnen de geest, door de rede kan worden gevonden en daardoor als verschijnsel uitsluitend binnen de geest wordt gekend. Alleen de menselijke geest is zich van dit verschijnsel in de natuur bewust.
De benaderende voorstelling, die de geest zich hiervan tracht te vormen, wordt een 'abstractie' genoemd. Dit woord is afkomstig van het Latijnse 'abstrahere', wat 'zich ervan aftrekken' betekent. Het houdt in dat de geest het vermogen bezit zich van de natuur los te maken, te abstraheren, om die vervolgens afstandelijk te beschouwen door in zichzelf de eigenschappen van de natuur te overdenken, te beoordelen en een plaats te geven.
Dat dit verschijnsel in de natuur bestaat, maar daar niet door de zintuigen heen kan worden opgemerkt, maar wel door de geest kan worden nagedacht, betekent, dat natuur en geest beide uit dezelfde bron zijn voortgekomen. Want, dat wij ménsen vermochten van de stóffelijke wereld de wiskúndige grondslag te ontdekken, wijst op beider wiskundige, dus gééstelijke oorsprong, daar wiskunde uitsluitend in de menselijke en goddelijke geest kan bestaan.
De grote geest, die in de mens Albert Einstein bij ons is geweest, deed in verband hiermee de uitspraak:
"Het meest onbegrijpelijke van het heelal is, dat wij het kunnen begrijpen!" en "Ik wil te weten komen, hoe God de wereld heeft gedacht!" *)
terug naar de Inhoud
2. Meetkunde en getaltheorie van de irrationele getallen
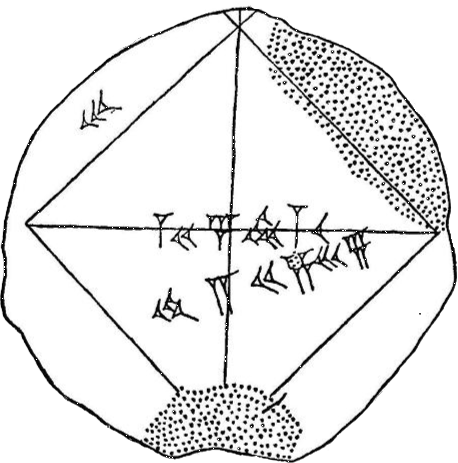
Algebra is in de loop der eeuwen uit de meetkunde voortgekomen. Bij de bouw van tempels en piramides werd door de Egyptenaren al van meetkunde gebruik gemaakt. De Soemeriërs/Babyloniërs hielden zich al bezig met het bepalen van de lengtes van meetkundige driehoeken en hadden al de regel gevonden, waarvoor later Pythagoras het bewijs leverde en daardoor naar hem de Stelling van Pythagoras werd genoemd: van een rechthoekige driehoek is het kwadraat van de schuine zijde gelijk aan de som van de kwadraten van de rechthoekszijden: a² + b² = c². Als voor de rechthoekszijden voor 1 wordt gekozen, dan is c² = 2. De grootte van c kan door worteltrekken √2 worden gevonden.
De Babyloniërs kenden al een goede benadering van √2 in de vorm van de breuk 30547/21600 = 1, 41421296... → ∞ (zie de kleitablet hierboven).
Iedere deling voegt een getal (decimaal) achter de komma toe, waarvan de waarde iedere keer weer 1/10e kleiner wordt. Daar de deling oneindig doorgaat, verliest de uitkomst van de deling zich in het oneindig kleine, maar houdt nooit op. De schuine lijn wordt in deze wereld met de lineaal wel getrokken en is zichtbaar, maar de waarde ervan is alleen binnen de geest met het verstand te beredeneren, niet te meten, onmeetbaar. De lijn bevindt zich in deze stoffelijke wereld, maar de werkelijke wáárde ervan is onbekend, want groeit aan met een oneindig kleiner wordend lijnstukje, wat alleen binnen de geest kan worden beschouwd en begrepen.(Kleitablet uit de tijd van koning Sargon, 2850 v. Chr.; links en rechts staan berekeningen)
Deze driehoek bevindt zich daardoor deels in de stoffelijke én in de geestelijke wereld, overeenkomend met het verschijnsel golf-deeltjedualiteit in de kwantumfysica. Het is een stoffelijk beeld met een geestelijke betekenis en deze pythagorese driehoek is daardoor een zinnebeeld van de eeuwige oneindigheid van √2, en daardoor van de geest in deze stoffelijke wereld.
Datzelfde geldt voor alle vier de driehoeken die de ruit vormen en daarin ook de diagonalen in de vorm van het gelijkbenige kruis.
Datzelfde geldt voor het gelijkbenige kruis met een omgeschreven cirkel bovenaan de afbeelding. De Babyloniërs wisten al dat de diameter van een cirkel ongeveer 3 1/7 keer om de omtrek past, wat leidt tot de breuk 22/7, waarvan ook hierbij de deling eeuwig door kan gaan tot in het oneindig kleine. Eenzelfde overweging als bij de wortel van 2 geldt ook hier. De omtrek van de cirkel kan wel in deze stoffelijke wereld met een passer worden getekend, maar de wáárde ervan bestaat alleen binnen de geest in de geestelijke wereld als de voorstelling van een eeuwig en oneindig voortdurende benadering.
Wordt de ruit een achtste slag gedraaid en over de cirkel met het gelijkbenige kruis gelegd, dan ontstaat een stervormige afbeelding ✳︎ , die zowel in Egypte als in Babylon zowel ster als God betekende (in Egypte was het in feite een vijfpuntige ster).Deze meetkundige, wiskundige figuren en daardoor figuren met een diepzinnige, geestelijke betekenis, waren in het Midden-Oosten wijd en zijd verspreid en bij alle volkeren bekend. Deze wiskundige beschouwingen waren er de oorzaak van, dat wiskunde en wijsbegeerte in die tijd naadloos met elkaar samenhingen.
Wiskunde is de kennis van datgene, wat 'gewis' is, wat zeker en daardoor betrouwbaar is. Wiskunde stond in de Oudheid in hoog aanzien, daar door het ontbreken van wetenschappelijke inzichten de wereld niet alleen vol wonderlijke zaken was, maar ook vol onbegrijpelijke, levensbedreigende gebeurtenissen, die het bestaan onzeker maakten. Wiskunde betekende daar tegenover een geruststellend houvast.
Geen wonder dat Jezus' volgelingen voor deze wiskundige afbeeldingen kozen om de betekenis van Jezus als hun rabbi, hun volstrekt betrouwbare godsdienstleraar weer te geven: in de mens Jezus was Gods heilige, volmaakte geest bij hen!
Betsaïda was een vissersplaatsje in het Noorden van Israël aan het Meer van Galilea, waar vier leerlingen vandaan kwamen en dat archeologisch is uitgegraven. Uit de tijd van Jezus vond men daar een thuissynagoge die als gebedsruimte door Jezus' volgelingen in gebruik moet zijn geweest en waar men op een steen een groot, gelijkbenig kruis aantrof.
Aan de overzijde van dat meer werden loden boekjes uit die tijd gevonden met een beschrijving van Jezus' leer en met dezelfde stervormige, gelijkbenige kruisen als een aanduiding van Jezus' godheid en wiskundige betrouwbaarheid.
Zie bij 'loden boekjes' in Vragen en antwoorden.
Het gelijkbenige kruis als
meetkundige figuur.
Zie bij 'loden boekjes' in Vragen en antwoorden.
Het gelijkbenige kruis als
meetkundige figuur.
Het gelijkbenige kruis als het aloude, kosmische zonnewiel; met daarin Pytha-goras' tetraktys: de vierheid als de eeuwige kringloop van het goddelijke gezin; daaromheen het vierkant als ruit met zijde √2 als de eeuwige, geestelijke werk-zaamheid van het goddelijke gezin als de gevórmde toestand;
de cirkel met π, de eeuwige, geestelijke werkzaamheid van de algeest in de óngevormde oertoestand; vervolgens: stel
r = 1, dan is het opp. van de ruit (√2)² = 2 en van de cirkel πr² = 3,1415... en hun verhouding 2/3,1415 = 0,636... terwijl
φ = 0,618... d.w.z. een fout van ±1%.
de cirkel met π, de eeuwige, geestelijke werkzaamheid van de algeest in de óngevormde oertoestand; vervolgens: stel
r = 1, dan is het opp. van de ruit (√2)² = 2 en van de cirkel πr² = 3,1415... en hun verhouding 2/3,1415 = 0,636... terwijl
φ = 0,618... d.w.z. een fout van ±1%.
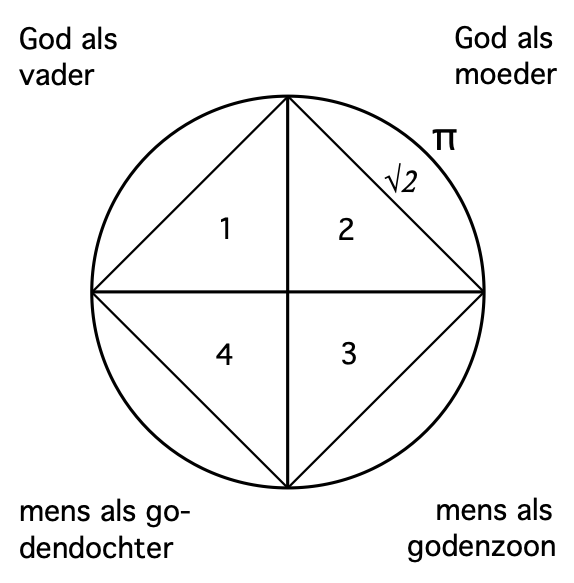
De verhouding van de oppervlakten van de ruit en de cirkel is een benadering van het getal φ van de gulden snede. Nu wordt in het boek van de ziener Jakob Lorber, De huishouding van God deel 3, uiteengezet (zie hier beneden) dat de plaats van God in de mensheid die is van de gulden snede. De gulden snede is een verhouding van twee lijnstukken, waarbij: het kleine deel staat tot het grote deel als het grote deel staat tot hun beider geheel. Dat kan worden toegepast op de verhouding tussen: de mens, Gods heilige geest - die in Jezus bij ons is geweest - en de goddelijke algeest als: de menselijke geest staat tot Gods heilige geest als de heilige geest staat tot de goddelijke algeest, hun geheel, of:
menselijke geest : heilige geest = heilige geest : algeest, dat is: b:a = a:(a+b).
Bovenstaande wiskundige afbeelding is daarmee een benaderend wiskundige afbeelding van Jezus' leer over de verhoudingen in Gods koninkrijk.
terug naar de Inhoud
3. Het getal φ phi van de gulden snede
Het getal φ van de gulden snede hangt nauw samen met de rij van Fibonacci: 1, 1, 2, 3, 5, 8 ,13, 21... die overal in de natuur, in Gods schepping, terug is te vinden. De verhouding wordt niet alleen door schoonheid gekenmerkt, maar ook door de meest efficiënte verdeling bijvoorbeeld van zaden over het bloembed, van bladeren langs de stengel i.v.m. regen en zonneschijn, de verhouding van afmetingen van lichaamsdelen in het menselijke lichaam, in de verhouding tussen de prime en de quint die de toonladder bepaalt, in kunstwerken, enz. (zie de 'Gulden Snede' in het Menu).
In onderstaand boek van de ziener en schrijver Jakob Lorber wordt een voorval beschreven uit de tijd, dat Jahwehs heilige geest zich aan sommigen op aarde vertoonde, zoals aan Henoch, Abraham en Mozes. Aan Abraham verscheen Jahweh in de vorm van drie engelen bij de eiken van Mamre (Gen. 18:1-15) om aan Sara en hem de geboorte van hun zoon Izaäk aan te kondigen; aan Mozes verscheen Jahweh meermalen tijdens de Exodus, de uittocht uit Egypte op de berg Horeb.
Later gebeurde dit bij de leerlingen na Jezus' opstanding en aan Paulus onderweg naar Damascus. Die ontmoeting maakte zo'n indruk op de Farizeeër Saulus, dat zijn houding geheel omsloeg en hij van christenvervolger nu met de naam Paulus een ijverige zendeling van Jezus werd.
In het boek van Jakob Lorber - De huishouding van God deel 3, hoofdstuk 61-62, wordt ook zo'n ontmoeting in het verre verleden van een aantal mensen met Gods heilige geest beschreven. Het gaat om Henoch, Lamech 'uit de hoogte' en Lamech 'uit de laagte'.
Tijdens een gesprek met hen wordt door God de polaire bouworde van zijn schepping besproken.
Die bouworde is niet een symmetrie, maar polair in de vorm van een lichtere noordpool en een zwaardere zuidpool. Het is dus een 'gebroken symmetrie' (zie de kwantumveldentheorie).
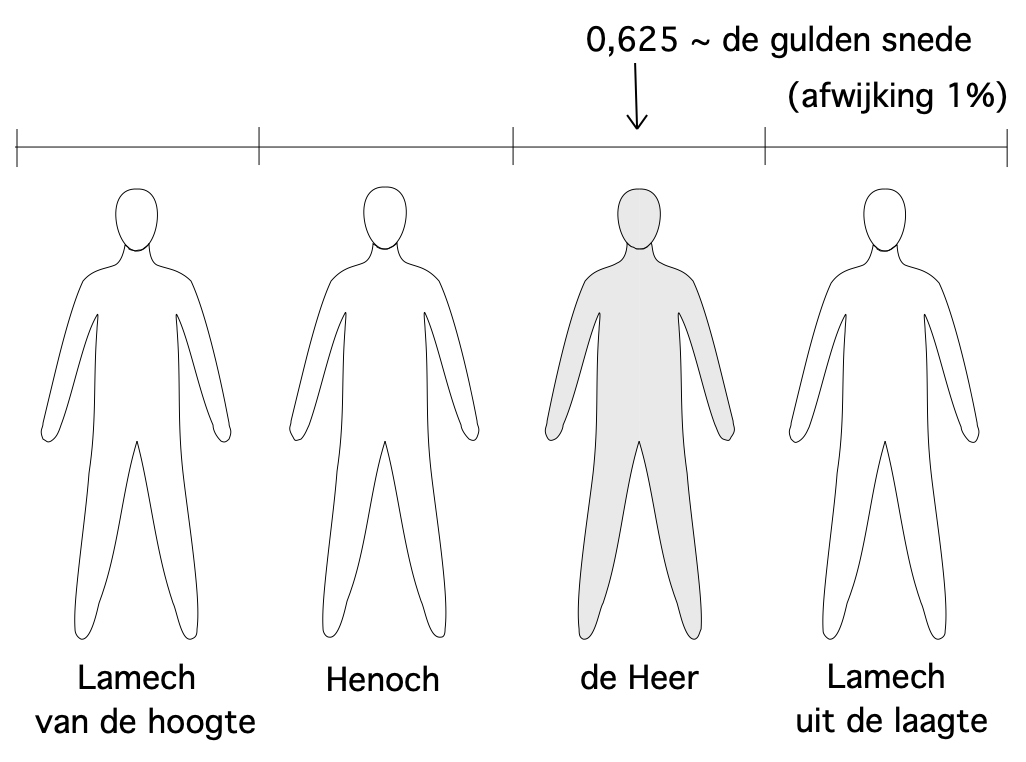Om de verhouding van die polen te beschrijven, gebruikt God de volgorde van vier zitplaatsen als een getallenlijn. Twee van de aanwezigen bij dit gesprek zitten aan de rechterkant van God, de derde aan de linkerkant. God als de grondslag van al het leven, bewegen en scheppen, bevindt zich op de derde plaats tussen de anderen in: dit is de juiste en goede ordening.De plaats die God inneemt heeft een verhouding die in de rij van Fibonacci 5:8 of 0,625 is. De breuk 0,625 is vrijwel die van de gulden snede: 0,618 (afwijking slechts 1%). Verderop in de rij benaderen de breuken van de getallen uit die rij (de termen) steeds meer de breuk van de gulden snede.
Ook φ is een irrationeel getal, waarvan de deling zich tot in de eeuwige oneindigheid voortzet en dat hier uitdrukkelijk wordt gebruikt om er de plaats van God in zijn schepping mee aan te duiden, de plaats die van de 'kosmos' is, wat: schoonheid, orde, regelmaat, samenhang, leiding, bestuur betekent.
In de boeken van Jakob Lorber treedt Gods heilige geest opnieuw op als godsdienstleraar voor de mensheid!
Bronnen:
Wikipedia
math4all.nl
maeckes.nl
wisfaq.nl
Alex Bellos; Getallen ontraadseld
vrijeschoolpedagogie.com/tag/babylonie
Jakob Lorber; De huishouding van God 3
*) "Het meest onbegrijpelijke aan het universum is, dat wij het kunnen begrijpen."
"The most incomprehensible thing about the universe is that it is comprehensible"
from "Physics and Reality" (1936), in Ideas and Opinions, trans. Sonja Bargmann (New York: Bonanza, 1954), p292. Cited by Frank Turek in "Stealing from God", pg 36
"Ik wil weten hoe God deze wereld heeft geschapen. Ik wil Zijn gedachten kennen, de rest zijn details."
"I want to know how God created this world .. I want to know His thoughts, the rest are details."
Quoted in Timothy Ferris, Coming of Age in the Milky Way, (N.Y., Morrow, 1988), 177.
terug naar de Inhoud
terug naar de serie 'godsaanwijzingen' in het Menu
terug naar het weblog
^