Yannick Fritschy - Grensverleggende getallen
Waarom de gulden snede het meest irrationale getal isDoor Yannick Fritschy, wetenschapsjournalist en redacteur bij New Scientist
Een samenvatting uit zijn boekje ‘Grensverleggende getallen’
Fibonacci en de gulden snede
De rij van Fibonacci is nauw verbonden met het getal Φ (Phi), beter bekend als de gulden snede. Φ Wordt gezien als het meest irrationale getal van allemaal.
Leonardo van Pisa, bijgenaamd Fibonacci, was een wiskundige uit de middeleeuwen. Hij is vooral bekend van de rij van Fibonacci. Dat is een getallenrij die begint met nul en één, waarbij je elk volgend getal krijgt door de vorige twee op te tellen: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ...
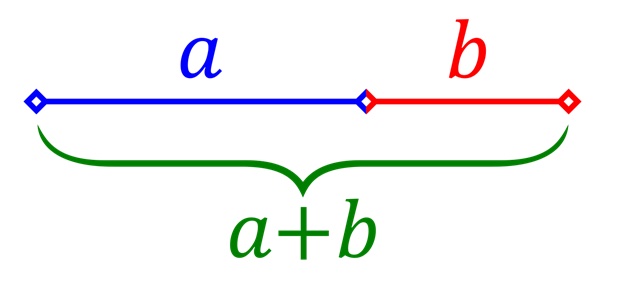
De rij van Fibonacci houdt verband met een van de bekendste getallen die er bestaan: de gulden snede. Dit getal krijg je wanneer je een lijnstuk zodanig in tweeën deelt, dat de verhouding tussen het grote en kleine deel hetzelfde is als de verhouding tussen het hele lijnstuk en het grote deel:
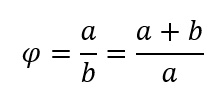
De verhouding tussen de lijnstukken is gelijk aan het getal van de gulden snede:
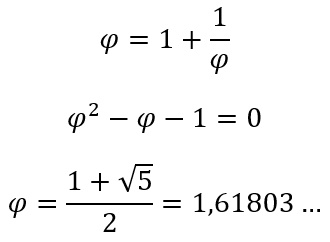Door deze formule te herschrijven, kun je de waarde van Φ uitrekenen:Dit getal bevat een eindeloze rij decimalen, zonder dat die zichzelf op een gegeven moment herhalen. Dat betekent dat je de gulden snede niet als gewone breuk kunt schrijven - dus niet als een deling tussen twee gehele getallen. Daarmee is Φ een irrationeel getal.
Op zichzelf is dat niet zo bijzonder. Er zijn veel meer irrationale dan rationale getallen. Andere bekende voorbeelden zijn π (3,14159...), het exponentiële getal e (2,71828...) en de wortel van twee (1,41421...).
Wat wel bijzonder is: volgens wiskundigen is de gulden snede het meest irrationale getal dat er bestaat.
Fibonacci en de fractale meetkunde
Dat komt doordat je de gulden snede Φ kunt schrijven als een zogeheten kettingbreuk. Dat is een breuk waarbij het 'Droste-effect' optreedt: een breuk in een breuk in een breuk in een breuk ... (een fractale recursie: terugloop)
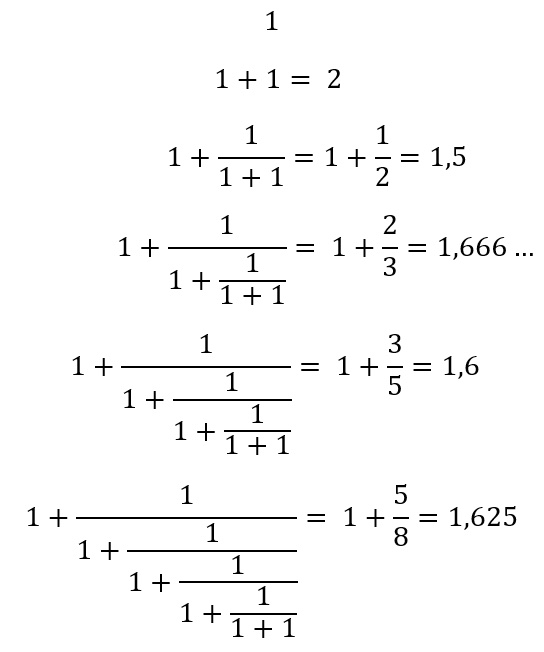Bij de gulden snede is de kettingbreuk op deze manier opgebouwd:Je ziet dat je ten slotte steeds dichter bij de echte waarde van Φ komt. Maar je komt er nooit helemaal; de kettingbreuk gaat eindeloos door. Dat maakt de gulden snede irrationeel.
Bovendien bevat deze breuk alleen maar enen. Daarmee is het een eindeloze kettingbreuk in zijn meest zuivere vorm. En daarom beschouwen wiskundigen de gulden snede als het meest irrationale getal.
Doen de meest rechter breuken in de vergelijkingen hierboven je trouwens ergens aan denken? Inderdaad: daar zie je het verband met de rij van Fibonacci.
Je kunt de gulden snede ook benaderen door twee opeenvolgende termen uit die rij door elkaar te delen. Het liefst zo hoog mogelijk: 89/55 is bijvoorbeeld 1,618181...
Het 'Droste-effect' is met de ontwikkeling van de fractale wiskunde ook uit wiskundig en wetenschappelijk oogpunt van belang geworden. Recursie (teruglopend) is een belangrijk principe van fractalen en het recursieve beeld op de Drostebus kan dan ook met recht een fractaal worden genoemd.
Met andere woorden:
Het verschijnsel fractaal hangt samen met de gulden snede, die een bijzondere fractaal is. De gulden snede kan worden geschreven als een z.g.n. kettingbreuk, door de getallen uit de rij van Fibonacci steeds te delen door het volgende getal. Daarbij treedt het z.g.n. 'Droste-effect' op: een breuk in een breuk in een breuk enz. Dat geeft een 'fractale recursie' weer (recursie: terugloop): een steeds herhaalde breuk, die zelfgelijkvormig is doordat de uitkomst steeds het getal φ (phi) is en waarvan (hier) de teller en noemer steeds groter worden.
Ook de opbouw van de Fibonacci-spiraal laat de fractale zelfgelijkvormigheid zien: een reeks van groter wordende vierkanten of gulden rechthoeken, waarbinnen de spiraal kan worden getekend.
terug naar het literatuuroverzicht
^